AbsoluteUnit
- 9
- 3
- TL;DR
- The Ackermann steering geometry is such that the lateral slip, tan(a) (where 'a' is the sideslip angle) tends to zero during stead-state low velocity turns. Is it reasonable to expect this vehicle behavior during simulation (see attached)?
Dear all,
I am writing a vehicle dynamics simulation for my thesis topic. However, I came into a conundrum when testing the cornering behavior of my vehicle. The problem is inherently complex due to its many subsystems, but I'll try to give as much detail without bogging the thread down.
Problem description
I am using a proprietary vehicle dynamics model to benchmark my own model. The issue is that I am finding discrepancies in the cornering behavior of my model and the proprietary model for the small turn angle, low-velocity case, but I am not entirely sure why. Essentially, my model exhibits a lower lateral displacement than predicted by the proprietary model and lower lateral acceleration, but the only reason I can think of is that the lateral slip of my tires aren't behaving similarly (after re-checking my equations multiple times) due to something else that I am missing.
My model is a front-steer vehicle that uses the Ackermann steering geometry to dictate the steer angle of the inner and outer tires (relative to the turn center). My understanding is that the Ackermann steer geometry is such that the vehicle can circumnavigate a curve at low (or zero) speeds without inducing a sideslip at the road-tire interface.
Since I haven't had much experience with vehicle modeling prior to this, I am looking for a second opinion on whether the following vehicle behavior looks "typical", or am I overlooking something very crucial? Should I just document my model's performance in the thesis and not worry so much about it?
Thank you for your insights.
(I did not attach the proprietary model output since I am just interested in whether the model behavior seems reasonable by intuition/prior experience. If it seems "off", that would at least give me an idea of whether I should be worried or not.)
---------------------------------
Scenario:
Initial longitudinal speed, Vx0 = 5 m/s
Initial lateral speed, Vy0 = 0 m/s
Initial angular speed, Psi0 = 0 rad/s
Input steer = 5 degrees (direct steer input, no steering ratio)
Wheel steers are recomputed for each wheel using the Ackermann steer ratio.
Vehicle properties
mass, m = 1778kg
yaw MoI, Jzz = 3800 kg-m^2
static weight distribution(front track/rear track) = approx. (9600N/7800N)
half-track width, w = 1m
front-track-to-centroid length, l1 = 1.33m
rear-track-to-centroid length, l2 = 1.62m
Centroid height = 0.53m
Load transfer is computed assuming a rigid vehicle model using the superposition of quasi-static longitudinal and lateral load shifts, i.e. without considering a suspension system.
Tire properties
Longitudinal slip stiffness, Cs = 89000 N/slip
Lateral slip stiffness, Ca = 45000 N/slip
static radius, Rg = 0.3m
Rolling MoI, Jyw = 2.00 kg-m^2
pavement friction coef., mu = 0.87
---
Two scenarios are attached:
(1) Turning without maintaining longitudinal velocity (no input torque)
(2) Turning with constant velocity
(1) Turning without maintaining longitudinal velocity (no input torque)
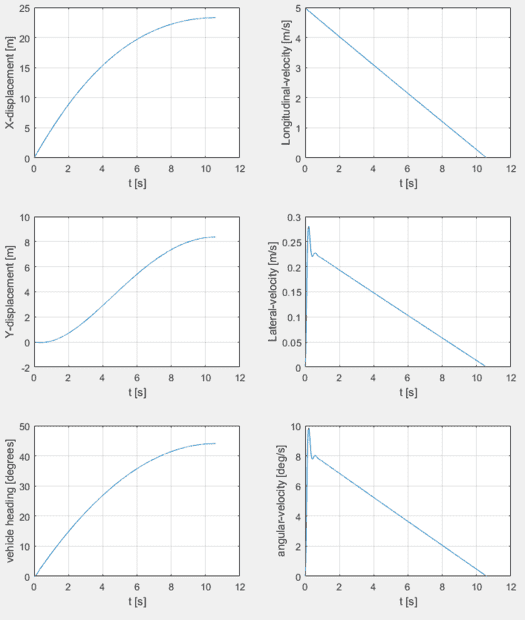
(left) Vehicle displacements (right) Vehicle-body velocities
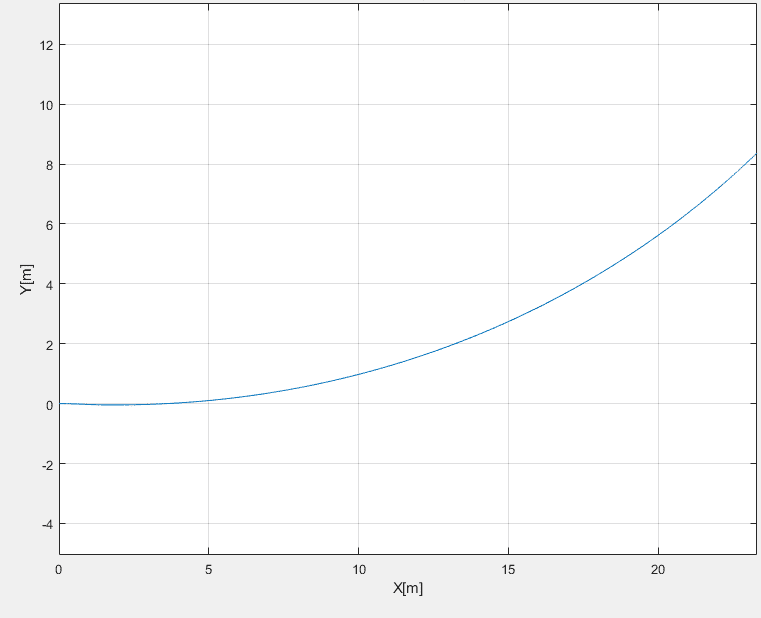
Vehicle trajectory
(2) Turning with constant longitudinal velocity
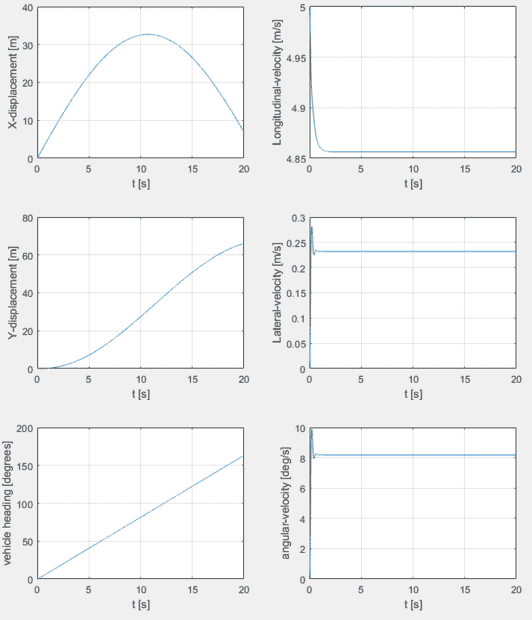
(left) Vehicle displacements (right) Vehicle-body velocities
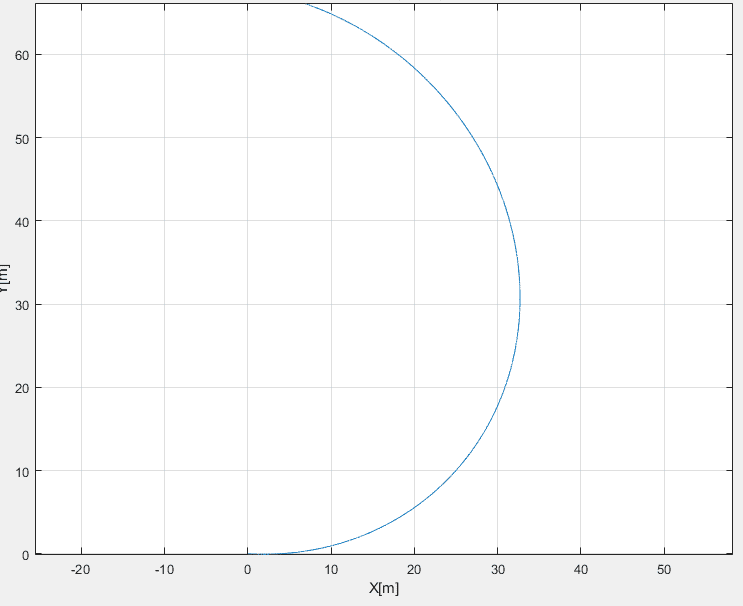
Vehicle trajectory
I am writing a vehicle dynamics simulation for my thesis topic. However, I came into a conundrum when testing the cornering behavior of my vehicle. The problem is inherently complex due to its many subsystems, but I'll try to give as much detail without bogging the thread down.
Problem description
I am using a proprietary vehicle dynamics model to benchmark my own model. The issue is that I am finding discrepancies in the cornering behavior of my model and the proprietary model for the small turn angle, low-velocity case, but I am not entirely sure why. Essentially, my model exhibits a lower lateral displacement than predicted by the proprietary model and lower lateral acceleration, but the only reason I can think of is that the lateral slip of my tires aren't behaving similarly (after re-checking my equations multiple times) due to something else that I am missing.
My model is a front-steer vehicle that uses the Ackermann steering geometry to dictate the steer angle of the inner and outer tires (relative to the turn center). My understanding is that the Ackermann steer geometry is such that the vehicle can circumnavigate a curve at low (or zero) speeds without inducing a sideslip at the road-tire interface.
Since I haven't had much experience with vehicle modeling prior to this, I am looking for a second opinion on whether the following vehicle behavior looks "typical", or am I overlooking something very crucial? Should I just document my model's performance in the thesis and not worry so much about it?
Thank you for your insights.
(I did not attach the proprietary model output since I am just interested in whether the model behavior seems reasonable by intuition/prior experience. If it seems "off", that would at least give me an idea of whether I should be worried or not.)
---------------------------------
Scenario:
Initial longitudinal speed, Vx0 = 5 m/s
Initial lateral speed, Vy0 = 0 m/s
Initial angular speed, Psi0 = 0 rad/s
Input steer = 5 degrees (direct steer input, no steering ratio)
Wheel steers are recomputed for each wheel using the Ackermann steer ratio.
Vehicle properties
mass, m = 1778kg
yaw MoI, Jzz = 3800 kg-m^2
static weight distribution(front track/rear track) = approx. (9600N/7800N)
half-track width, w = 1m
front-track-to-centroid length, l1 = 1.33m
rear-track-to-centroid length, l2 = 1.62m
Centroid height = 0.53m
Load transfer is computed assuming a rigid vehicle model using the superposition of quasi-static longitudinal and lateral load shifts, i.e. without considering a suspension system.
Tire properties
Longitudinal slip stiffness, Cs = 89000 N/slip
Lateral slip stiffness, Ca = 45000 N/slip
static radius, Rg = 0.3m
Rolling MoI, Jyw = 2.00 kg-m^2
pavement friction coef., mu = 0.87
- The Dugoff tire model was used to compute tire forces.
- The force curves produced were qualitatively similar to the force curves produced by the proprietary model.
- The slip stiffness are assumed to be static (i.e. not load-sensitive).
---
Two scenarios are attached:
(1) Turning without maintaining longitudinal velocity (no input torque)
(2) Turning with constant velocity
(1) Turning without maintaining longitudinal velocity (no input torque)
(left) Vehicle displacements (right) Vehicle-body velocities
Vehicle trajectory
(2) Turning with constant longitudinal velocity
(left) Vehicle displacements (right) Vehicle-body velocities
Vehicle trajectory