maistral
- 235
- 17
Hi, just a question regarding neumann conditions, I seem to have forgotten these things already. I think this question is answerable by a yes or a no.
So given the 2D heat equation,
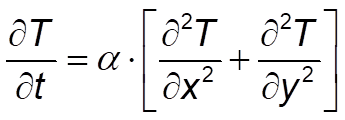
If I assign a neumann condition at say, x = 0;
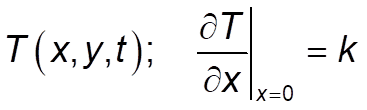
Does it still follow that at the derivative of t, the condition still holds? I mean:
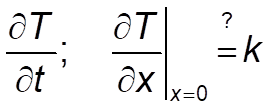Thank you!
So given the 2D heat equation,
If I assign a neumann condition at say, x = 0;
Does it still follow that at the derivative of t, the condition still holds? I mean: