Ark236
- 24
- 3
- Homework Statement
- Hi everyone,
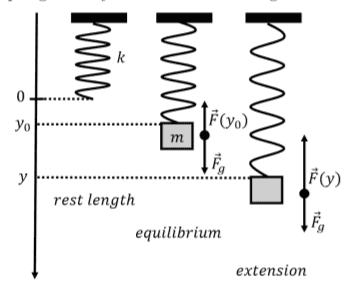
The problem has two parts. The first is to determine the equilibrium position of a mass attached to a spring. The second is to determine the equation of motion of the system, assuming that the block is pulled 1 cm down from its equilibrium position.
- Relevant Equations
- I choose the downward direction as positive. For the first part and using the FBD:
mg - k y_{0} = 0
Then the equilibrium position is y_{0} = mg/k.
For the second part, we have that:
mg -k y = m d^2 y/dt^2
I have a doubt with the last part. Why isn't the right side negative? Because when the block is released, it moves upwards.
thanks
image was obtained from here
Thanks.
thanks
image was obtained from here
Thanks.