Virtual Work in a Pulley System

[lowea001]

Homework Statement

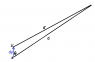
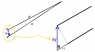
The system shown in Fig. 2-6 is in static equilibrium. Use the principle of virtual work to find the weights A and B. Neglect the weight of the strings and the friction in the pulleys.

Quick aside: This is straight out of the Exercises for the Feynman Lectures on Physics, in which he introduces virtual work as an imaginary displacement that let's us find the weight or height of objects in what he calls a "reversible machine".

I know how to do this equilibrium problem using force vectors, but am not sure where to begin with virtual work. Can anyone help me to solve the question using this method?

Homework Equations

Ug = mgh
Total Ug = 0[/B]

The Attempt at a Solution

Right off the bat I know the answer to this question, I'm desperate for a solution/explanation.

I begin by imagining the 1kg weight falls 1 unit, which means that weight A must rise 1/2 a unit based on the angle of the string. Then I don't know whether or not I should include weight B in this displacement, or if it should fall, or if the entire right side of the system should rise according to the displacement of weight A in order to preserve the geometry of the system. After a bit of easy mathy stuff you can get the equation 0 = -1(1) + 1/2(A) + (whatever B does)B. I've tried many different imaginary displacements for B, but can't seem to get the right answer. This isn't very difficult using force vectors, but the question specifically asks for it to be solved using the method of virtual work, which I am admittedly unfamiliar with. What do I have to imagine the system does here? Maybe my original guess that weight A should rise a distance of Sin30 is wrong as well.

 

[TSny]

Did you try virtual displacements of the knot where the three strings meet?

If the knot is moved horizontally by an infinitesimal amount $\delta x$, what are the vertical displacements of the three masses to first order in $\delta x$?

Similarly, what happens if the knot is displaced vertically by $\delta y$?

What do you mean when you state that "Total U_g = 0"? How do you use that?

 

[lowea001]

Did you try virtual displacements of the knot where the three strings meet?

If the knot is moved horizontally by an infinitesimal amount $\delta x$, what are the vertical displacements of the three masses to first order in $\delta x$?

Similarly, what happens if the knot is displaced vertically by $\delta y$?

What do you mean when you state that "Total U_g = 0"? How do you use that?

Sorry, I meant to say that the total W_g = 0, not the energy. So if I move the weight A down by an infinitesimally small 1 unit, then the 1kg weight must move up 2 units and weight B must move up √2 units. This gives me A = 2 + √2(B). My mistake is somewhere here. If I perform a horizontal displacement of 1 unit right, weight B must move down √2 units and the 1kg weight must move up (doing the math) 2/√3 units. Weight A is horizontally displaced so it remains at the same height. This gives me B = 2/√6, which I know is incorrect. Where did I go wrong? Am I doing virtual work incorrectly? Thanks for your help so far. :)

 

[TSny]

Sorry, I meant to say that the total W_g = 0, not the energy. So if I move the weight A down by an infinitesimally small 1 unit, then the 1kg weight must move up 2 units and weight B must move up √2 units.

You have the right idea that the total work done by gravitational forces will be zero for a virtual displacement.

However, your calculations of the displacements of B and the 1 kg mass are not correct. Can you explain how you got these answers?

 

[lowea001]

You have the right idea that the total work done by gravitational forces will be zero for a virtual displacement.

However, your calculations of the displacements of B and the 1 kg mass are not correct. Can you explain how you got these answers?

To be honest, not very well. I may have made many false assumptions as the whole concept of imaginary work confuses me at the moment. I know that weight A can be said to move down 1 really small unit. From there, I need to know the changes in heights of the other weights, and multiply all the weights by their respective changes in heights and equate them to zero. I know that if weight A moves down 1 unit and the angle 30° is preserved, the string must have been translated a distance of 2 units because 1/Sin30 = 2 = hyp = distance the string moved. Is this a false assumption? Or is the assumption that the angles are preserved false? I think I'm getting warmer. Kinda.

 

[lowea001]

Or maybe I need to use Pythagorean theorem.

 

[TSny]

Suppose the knot is moved vertically upward a distance dy from point a to point a' as shown below. The portion of the string that goes from the knot to the right pulley changes length from d to d'. Can you work out how much shorter d' is than d? You just need to get an expression that is accurate to first order in dy.

 

[haruspex]

Or maybe I need to use Pythagorean theorem.

The method I use is to think in terms of displacement (or velocity) components. If the knot above A moves straight down at some rate, what is the component of that in the direction of string going up to the left hand pulley? What is its component perpendicular to that string? Which of these will turn the pulley?

 

[TSny]

The method I use is to think in terms of displacement (or velocity) components. If the knot above A moves straight down at some rate, what is the component of that in the direction of string going up to the left hand pulley? What is its component perpendicular to that string? Which of these will turn the pulley?

Yes, that's a nice way to think about it.

 

[lowea001]

Yay I finally solved the question, thanks a lot guys. By doing what haruspex suggested, I found the components of the virtual velocities/displacement vectors that ran in the same direction as the pulley strings. Moving the knot horizontally means that the height of A doesn't change and you can just solve for B based on what the 1kg weight does and equating the total work done to 0. Then, I can substitute the value for B into the equation you get for the total work done from a vertical virtual velocity/displacement. Basically, it wasn't too tough after all. Thanks for your guidance.

Just out of curiosity Tsny, how would you find out how much shorter d' was than d in your diagram? Would you connect d to a' with a line perpendicular to d and treat the base of that triangle as the distance you're looking for?

 

[TSny]

Just out of curiosity Tsny, how would you find out how much shorter d' was than d in your diagram? Would you connect d to a' with a line perpendicular to d and treat the base of that triangle as the distance you're looking for?

Yes! Since dy is infinitesimal, the lines d and d' will be approximately parallel to the accuracy we need. So, dropping that perpendicular line as you suggest will give the the difference between d and d'. (See figure below.) d-d' will be how much mass B moves down.

 

[soj]

My approach was that the situation was to be considered in equilibrium, that is that A should oppose 2 equal horizontal forces in opposite directions:
being (1/2 . sqrt 3) on the left and (1/sqrt2 times B) on the right, giving B = sqrt3/sqrt2.
For A to stay in place and not being pulled up, its weight shoud equal the sum of the 2 vertical components of the left and right blocks, being left:(1/2) and right (1/sqrt2 times B).
The question asked was to explain things in terms of virtual work. Do I need to perform a thought experiment of moving the blocks, and if so how should that be done ?

 

[haruspex]

I need to perform a thought experiment of moving the blocks, and if so how should that be done ?

That is explained in posts #2 and #8.