Viscosity in lubricating fluid in the bench-guide of a machine

[Guillem_dlc]

Homework Statement

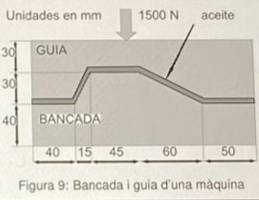
The bench-guide of a machine (see figure) has the cross-section shown in the figure and an extension $L=60\, \textrm{cm}$. The force exerted by the weight supported by the bench is $1500\, \textrm{N}$ and the bench moves (in a direction perpendicular to the figure) at a constant speed $c=6000\, \textrm{mm}/\textrm{min}$. The clearance between the bench and the guide is $h=0,1\, \textrm{mm}$ and it is assumed to be filled with a lubricating oil of viscosity $\nu =5\, \textrm{stoke}$ and relative density $\rho_r=0,9$. Calculate:

a) the shear stress $\tau$, at $\textrm{N}/\textrm{m}^2$. Solution: $\tau =450\, \textrm{N}/\textrm{m}^2$

b) The power $P$, in $\textrm{W}$, required to overcome the frictional resistance of the fluid. Solution: $P=6,361\, \textrm{W}$

c) The dynamic viscosity $\mu$ of the lubricant, in \textrm{decapoise} if, if it is desired to reduce the above power by $5\%$. Solution: $\mu =0,4274\, \textrm{kg}/(\textrm{m}\cdot \textrm{s})$

Relevant Equations

$v=\dfrac{\mu}{\rho}$, $\tau =\mu \dfrac{c}{h}$

Figure: bench (bancada), guide (guide), oil (aceite).

My attempt at a solution:
$$\textrm{extension } L=0,6\, \textrm{m}$$
$$F=1500\, \textrm{N},\,\, c=0,1\, \textrm{m}/\textrm{s},\,\, h=0,0001\, \textrm{m}$$
$$v=5\, \textrm{stoke}=0,0005\, \textrm{m}^2/\textrm{s},\,\, \rho_r=0,9$$
a) $$\rho_r=\dfrac{\rho}{\rho_{\textrm{H2O}}}\rightarrow \rho =900\, \textrm{kg}/\textrm{m}^3$$
We calculate the area of the bench:
$$v=\dfrac{\mu}{\rho}\rightarrow \mu =v\rho =0,45\, \textrm{Pa}\cdot \textrm{s}$$
$$\tau =\mu \dfrac{c}{h}\rightarrow \boxed{\tau =450\, \textrm{N}/\textrm{m}^2}$$

I have tried to do this. And b) and c) I have no idea how to approach them.

 

[erobz]

I'm not sure I fully have been able to factor in all the parameters, but for starters let's see if we can get you closer than "I have no idea" for part (b).

Do a force balance in the direction of motion, for the guide. What do you get for the force of the required push ( in all variables - no numbers)?

 

[Guillem_dlc]

I'm not sure I fully have been able to factor in all the parameters, but for starters let's see if we can get you closer than "I have no idea" for part (b).

Do a force balance in the direction of motion, for the guide. What do you get for the force of the required push ( in all variables - no numbers)?

I've done this, look:

b) Find hypotenuse: $H^2=c_1^2+c_2^2$
$$A=(0,04+\sqrt{0,015^2+0,03^2}+0,045+\sqrt{0,06^2+0,03^2}+0,05)\cdot 0,6=0,14137\, \textrm{m}^2$$
$$F=\tau \cdot A=63,62\, \textrm{N}$$
Because we have constant velocity:
$$\boxed{P=F\cdot c=6,362\, \textrm{W}}$$

c) We reduce $5\% \rightarrow P'=6,0439\, \textrm{W}$
$$P'=F'c\rightarrow F'=\dfrac{P'}{c}=\tau' A\rightarrow \tau' =\dfrac{P'}{cA}\rightarrow$$
$$\mu' \dfrac{c}{h}=\dfrac{P'}{cA}\rightarrow \boxed{\mu '=\dfrac{P'h}{c^2A}=0,4275\, \textrm{Pa}\cdot \textrm{s}}$$

 

[erobz]

I've done this, look:

b) Find hypotenuse: $H^2=c_1^2+c_2^2$
$$A=(0,04+\sqrt{0,015^2+0,03^2}+0,045+\sqrt{0,06^2+0,03^2}+0,05)\cdot 0,6=0,14137\, \textrm{m}^2$$
$$F=\tau \cdot A=63,62\, \textrm{N}$$
Because we have constant velocity:
$$\boxed{P=F\cdot c=6,362\, \textrm{W}}$$

c) We reduce $5\% \rightarrow P'=6,0439\, \textrm{W}$
$$P'=F'c\rightarrow F'=\dfrac{P'}{c}=\tau' A\rightarrow \tau' =\dfrac{P'}{cA}\rightarrow$$
$$\mu' \dfrac{c}{h}=\dfrac{P'}{cA}\rightarrow \boxed{\mu '=\dfrac{P'h}{c^2A}=0,4275\, \textrm{Pa}\cdot \textrm{s}}$$

I'm confused. Those look like the answers to me?

 

[Guillem_dlc]

I'm confused. Those look like the answers to me?

This is what I have tried to do for (b) and (c).

 

[erobz]

This is what I have tried to do for (b) and (c).

You are saying those are not correct? Do you have the correct answers for part (b) and (c)?

 

[Guillem_dlc]

You are saying those are not correct? Do you have the correct answers for part (b) and (c)?

I don't know if the steps I have done are correct or not. This I what I'm asking.

 

[erobz]

I don't know if the steps I have done are correct or not. This I what I'm asking.

The steps seem logical to me.

 

[erobz]

Where does the $1500 \rm{N}$ force factor in? That is what I am unsure about. I feel like the shear stress should be a function of the load.

 

[Guillem_dlc]

Where does the $1500 \rm{N}$ force factor in? That is what I am unsure about. I feel like the shear stress should be a function of the load.

We don't care, do we? Because it does not run parallel to this force.

 

[erobz]

We don't care, do we? Because it does not run parallel to this force.

I don't know. Does shear stress have dependencies on fluid pressure? Intuitively I feel like it should, but perhaps it doesn't.

I'm just kind of paralleling the idea from solid mechanics that the frictional force is dependent on the Normal force, and the shear stress might be dependent on pressure in a similar manner.

If there is no dependency (or it's not an issue until extreme pressures), then it seems fine that the $1500 \rm{N}$ is ignorable.

 

[Guillem_dlc]

I don't know. Does shear stress have dependencies on fluid pressure? Intuitively I feel like it should, but perhaps it doesn't.

I'm just kind of paralleling the idea from solid mechanics that the frictional force is dependent on the Normal force, and the shear stress might be dependent on pressure in a similar manner.

If there is no dependency (or it's not an issue until extreme pressures), then it seems fine that the $1500 \rm{N}$ is ignorable.

Ok ok

 

[erobz]

The gauge pressure from the load is pretty small in comparison to atmospheric...there is probably no effect to consider. I'm not trying to steer you into left field, it's just something that I wasn't sure about.

 

[Lnewqban]

I don't know. Does shear stress have dependencies on fluid pressure? Intuitively I feel like it should, but perhaps it doesn't.

I'm just kind of paralleling the idea from solid mechanics that the frictional force is dependent on the Normal force, and the shear stress might be dependent on pressure in a similar manner.

If there is no dependency (or it's not an issue until extreme pressures), then it seems fine that the $1500 \rm{N}$ is ignorable.

Please, see:
https://www.engineeringtoolbox.com/dynamic-absolute-kinematic-viscosity-d_412.html

 

[Guillem_dlc]

Please, see:
https://www.engineeringtoolbox.com/dynamic-absolute-kinematic-viscosity-d_412.html

Ok perfect now I will take a look at it! Thanks

 

[erobz]

Please, see:
https://www.engineeringtoolbox.com/dynamic-absolute-kinematic-viscosity-d_412.html

"The shear resistance in a fluid is caused by inter-molecular friction exerted when layers of fluid attempt to slide by one another."

Its not clear with this statement from the link why there wouldn't be some pressure dependence in the shear stress in my opinion. That being said, my fluids text doesn't bring up the possible effect of pressure on shear stress either. If there is any effect, it's probably negligible for any reasonable pressures.

 

[Lnewqban]

"The shear resistance in a fluid is caused by inter-molecular friction exerted when layers of fluid attempt to slide by one another."

Its not clear with this statement from the link why there wouldn't be some pressure dependence in the shear stress in my opinion. That being said, my fluids text doesn't bring up the possible effect of pressure on shear stress either. If there is any effect, it's probably negligible for any reasonable pressures.

Excellent remark!
You may find this lecture interesting:
https://galileo.phys.virginia.edu/classes/152.mf1i.spring02/Viscosity.pdf