MATLAB Visualizing a Segment of a Unit Circle

[chrisych]

a = 60*pi/180;
a1 = (pi - a)/2;
a2 = (pi + a)/2;
theta = a1: a/60: a2;
rho = ones(size(theta));
rho1 = rho*sin(a1)./sin(theta);
polar(theta, rho);
hold on;
polar(theta, rho1)

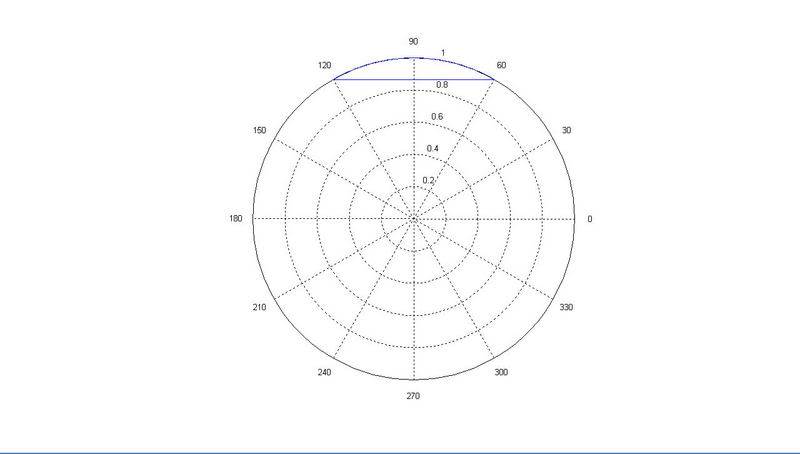
The above commands will draw a segment of a unit circle which starts from 60^{o} to 120^{o}.

I know everything except the line of "rho1 = rho*sin(a1)./sin(theta);" that I don't know why this equation works from 1 --> 0.866 --> 1 and becomes a straight line. Can anyone tell me the reason? Is it related to a similar triangle or inverse proportion?

 

[neurocomp2003]

try converting from polar to euclidean/cartesian...to see if you can figure out how they got that straight line. Remember what does rho,rho1 stand for in polar.

 

[chrisych]

Cartesian to Polar:
r = sqrt(x^2 + y^2)
theta = arctan(y/x)

Polar to Cartesian:
x = r cos theta
y = r sin theta

rho = 1 (for unit circle)

rho1 = rho*sin(a1)/sin(theta) = 1*sin(60)/sin(60) to 1*sin(60)/sin(120) = 1 --> 0.866 --> 1

 

[girlsridemx2]

Write the equation of a rational function that has vertical asymptotes at x=2 and x=3 and a horizontal asymptote at y=2

yeah, i really need help with this problem. Thanks so much