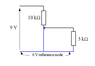
Discussion Overview
The discussion revolves around determining the voltage across a potentiometer with a specific load and finding the position of the slider when the voltage at certain points is given. Participants explore various methods to analyze the circuit, including the use of voltage divider rules and the relationships between resistances in the circuit.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
- Homework-related
Main Points Raised
- Some participants express confusion about how to find the current without knowing the total resistance of the circuit.
- Others suggest writing equations for the output voltage in terms of the wiper position and using variables to represent the fractions of the potentiometer's resistance.
- One participant proposes considering the potentiometer as two separate resistors to simplify analysis.
- Several participants discuss the application of the voltage divider rule and the need to account for the load resistor in calculations.
- Some participants question the correctness of their equations and seek clarification on how to properly apply the voltage divider rule.
- There are multiple attempts to derive the correct equations, with some participants reporting different values for the wiper position.
- One participant mentions struggling to simplify their equations and seeks guidance on the algebra involved.
- Another participant emphasizes the importance of starting from the circuit diagram and deriving the equations step by step.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the correct approach or final answer. There are multiple competing views on how to analyze the circuit, and several participants express uncertainty about their calculations and the application of the voltage divider rule.
Contextual Notes
Some participants note that earlier posts contained incorrect assumptions or equations, and there is a general acknowledgment of the complexity involved in deriving the correct expressions. The discussion includes various mathematical steps that remain unresolved, and participants express differing results for the wiper position.