unknownv2
- 1
- 0
(Sorry, meant to post this in Introductory Physics Homework, if someone could please move it.)
1. Homework Statement
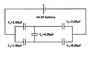
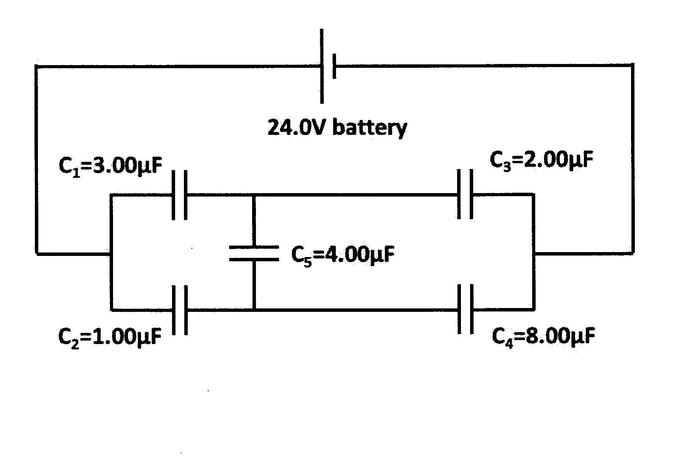
Use Kirchhoff's Loop Rule to solve for the voltages of the five capacitors in the network shown below.
For Capacitance, C = q/v
Kirchoff's juction law states that the total current into a junction must equal the total current leaving the function and that the sum of the potential differences around any loop or closed path is zero.
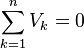
[/B]
My work can be found here: (Warning large image)
https://i.imgur.com/RMDZrAP.jpg
The solution requires a system of equations to solve and I have:
1) ## -V_1 - V_5 - V_2 + V_A = 0##
2) ## -V_3 - V_5 - V_4 + V_A = 0##
3) ## -Q_5 + Q_4 + Q_2= 0##
4) ## -Q_1 - Q_3 + Q_5= 0##1 and 2 translate to:
1) ##\frac{-Q_1}{C_1} + \frac{-Q_5}{C_5} + \frac{-Q_2}{C_2} + 24 = 0##
2) ##\frac{-Q_3}{C_3} + \frac{-Q_5}{C_5} + \frac{-Q_4}{C_4} + 24 = 0##
It doesn't seem possible to solve those system of equations so I assume I messed up somewhere on creating the equations.Questions:
1) Can an open/close loop be created by the voltage connections on both sides of the capacitor, without necessarily returning to the original entrance of the voltage? Such as, if the voltage enters on the left side, can it leave through the right? I'm thinking enters from left (##V_L##) to ##C_1## through ##C_5## then ##C_4## then out the right (##V_R##) side, as an example?
2) How many equations would be needed for the system of equations? Does that depend on the number of junctions or the number of capacitors? So would I need 5 equations total before I can solve this?
1. Homework Statement
Use Kirchhoff's Loop Rule to solve for the voltages of the five capacitors in the network shown below.
Homework Equations
For Capacitance, C = q/v
Kirchoff's juction law states that the total current into a junction must equal the total current leaving the function and that the sum of the potential differences around any loop or closed path is zero.
The Attempt at a Solution
[/B]
My work can be found here: (Warning large image)
https://i.imgur.com/RMDZrAP.jpg
The solution requires a system of equations to solve and I have:
1) ## -V_1 - V_5 - V_2 + V_A = 0##
2) ## -V_3 - V_5 - V_4 + V_A = 0##
3) ## -Q_5 + Q_4 + Q_2= 0##
4) ## -Q_1 - Q_3 + Q_5= 0##1 and 2 translate to:
1) ##\frac{-Q_1}{C_1} + \frac{-Q_5}{C_5} + \frac{-Q_2}{C_2} + 24 = 0##
2) ##\frac{-Q_3}{C_3} + \frac{-Q_5}{C_5} + \frac{-Q_4}{C_4} + 24 = 0##
It doesn't seem possible to solve those system of equations so I assume I messed up somewhere on creating the equations.Questions:
1) Can an open/close loop be created by the voltage connections on both sides of the capacitor, without necessarily returning to the original entrance of the voltage? Such as, if the voltage enters on the left side, can it leave through the right? I'm thinking enters from left (##V_L##) to ##C_1## through ##C_5## then ##C_4## then out the right (##V_R##) side, as an example?
2) How many equations would be needed for the system of equations? Does that depend on the number of junctions or the number of capacitors? So would I need 5 equations total before I can solve this?
Attachments
Last edited: