Equivalent capacitance of a system from potential difference

[Soren4]

Homework Statement

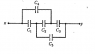
Calculate the equivalent capacity of the capacitor system between points $x$ and $y$

Homework Equations

$C=q/V$

The Attempt at a Solution

I'm asking about this problem because I know how to calculate $V_x-V_y$, but I don't know how can I extract the equivalent capacity from there.
Using Kirchoff Laws I get the following equations

1. $$V_x-V_y=q_1/C_1+q_2/C_2+q_3/C_3 $$
   
2. $$V_x-V_y=q_4/C_4+q_3/C_3 $$
   
3. $$V_x-V_y=q_1/C_1+q_5/C_5 $$
   
4. $$0=-q_1/C_1-q_2/C_2+q_4/C_4 $$
5. $$0=q_2/C_2+q_3/C_3-q_5/C_5 $$

($1,2,3$ express $V_x-V_y$ through all the possible paths from $x$ to $y$ I can take, while $4,5$ are loop laws for the two loops).

I can solve for $V_x-V_y$, but then here it comes the doubt.

As said I have three different ways to go from $x$ to $y$ (the first three equations are there because of that), I highlighted them in the picture (path $A$ is equation $1$, path $B$ is equation $2$, path $C$ is equation $3$)

So can I express the equilvalent capacitance of the system as the ratio of the charge met following the particular path and $V_x-V_y$? That would be

$$C_{equivalent}=(q_1+q_2+q_3)/V_x-V_y=(q_4+q_3)/V_x-V_y=(q_1+q_5)/V_x-V_y$$

This does not look correct at all, but it is the only reasonable way to use the potential difference to calculate capacity.

So I ask: what is the right way to link $V_x-V_y$ to $C_{equivalent}$? That is : how to calculate $C_{equivalent}$ knowing $V_x-V_y$?

I would like to use this method (using $V_x-V_y$) and not other ones (if there are any) because I would like to understand how it should work, so please help me figure out the link between $V_x-V_y$ and $C_{equivalent}$ in cases like this one.

 

[gneill]

One of the problems is that for a capacitor like C2 you can't be sure which way it's polarity is going to end up. It will depend upon the values of the other capacitors around it, which create voltage dividers.

What you can do is write mesh equations for the charges (as opposed to currents). When some hypothetical voltage is placed across xy then there will be a brief transient time during which currents flow to move the charges to their steady state locations. Assign "mesh charges" to each loop and write KVL. Solve for the mesh charge associated with the voltage supply loop.

KVL will sort out all polarity issues for you, all you need to do is respect the mesh charge directions while writing the equations.

 

[Soren4]

Thanks for your answer and the clear picture! I'm also learning how to use KVL properly, nevertheless I asked just because of the equivalent capacitance of the system between points $x$ and $y$.

Suppose that, using KVL, I find out $V_x-V_y$. Then how do I calculate $C_{EQUIVALENT \, x \to y }$ (the equivalent capacitance of the system between points $x$ and $y$)? Can I do what I showed in the question (divide the charge met on a particular path by $V_x-V_y$)?

 

[gneill]

Thanks for your answer and the clear picture! I'm also learning how to use KVL properly, nevertheless I asked just because of the equivalent capacitance of the system between points $x$ and $y$.

Suppose that, using KVL, I find out $V_x-V_y$. Then how do I calculate $C_{EQUIVALENT \, x \to y }$ (the equivalent capacitance of the system between points $x$ and $y$)? Can I do what I showed in the question (divide the charge met on a particular path by $V_x-V_y$)?

Well, $V_x-V_y$ is going to be constrained by the voltage source V. No matter what the capacitance is between x and y the potential difference will be enforced by the voltage source, so that voltage in and of itself gives no information about the actual capacitance value.

What will tell you the capacitance is working out how much charge moved from the voltage source to the circuit ($q_1$ in my diagram). If you could somehow determine the charges on C1 and C4, or on C3 and C5 then you would have that, since any charge from the source must flow through those pairs; there are no other paths available. But again C2 is a problem, since you don't know how it's going to affect the charge splitting on the "important" pairs. That leaves you with writing equations to solve the problem.

You need to write simultaneous equations to figure out how much charge moved where. That, I presume was the point of your attempt in your first post, writing the sum of the potential changes along a few of the paths. But it's tricky to write a consistent set of equations when you have to guess at some of the charge flow directions. That's why I suggested a methodical plan like using mesh equations. Nodal equations probably work as well; the circuit has just two essential nodes.

 

[gneill]

As a point of interest, the given circuit can be redrawn in the form of a "bridge" circuit:

 

[rude man]

Homework Statement

Calculate the equivalent capacity of the capacitor system between points $x$ and $y$
View attachment 107985

Homework Equations

$C=q/V$

The Attempt at a Solution

I'm asking about this problem because I know how to calculate $V_x-V_y$, but I don't know how can I extract the equivalent capacity from there.
Using Kirchoff Laws I get the following equations

1. $$V_x-V_y=q_1/C_1+q_2/C_2+q_3/C_3 $$
   
2. $$V_x-V_y=q_4/C_4+q_3/C_3 $$
   
3. $$V_x-V_y=q_1/C_1+q_5/C_5 $$
   
4. $$0=-q_1/C_1-q_2/C_2+q_4/C_4 $$
5. $$0=q_2/C_2+q_3/C_3-q_5/C_5 $$

You have 5 independent equations in 5 unknowns (Vy-Vx is arbitrary) so here's the hint: solve for and work with q1 + q4.
EDIT: oops, you don't. 2 of the 5 are redundant.
So get rid of two redundant ones and then you have to also consider current flow. Remember that current flow determines charge. So for example you can argue that q1 = q2 + q5 by summing currents to zero at the C1-C5 junction. Another hint: how are q1 + q4 related to q3 + q5?

 

[Soren4]

@gneill Thanks so much for the clear answer to the question! To sum up, in this case, can I determine the equivalent capacity by the following?

$$C_{eq, x\to y}=\frac{q_1+q_4}{V_x-V_y}=\frac{q_3+q_5}{V_x-V_y}$$

And can I evaluate the charges I need (e.g. $q_1$ and $q_4$ ) by using mesh equations?

The ones I wrote in the question were intended to be mesh equations for the two loops (not including the one with the generator), plus generalized Ohm law for all the possible paths from $x$ to $y$: the sign of charges were assignet arbitrary for Ohm law (as showed in the picture the positive charge is always the one on the left face of capacitor). The choice of positive charges was respected in the two loop equation, orienting both loops clockwise and considering the sign of the charge firstly met on each capacitor while moving around the loop clockwise.

 

[gneill]

@gneill Thanks so much for the clear answer to the question! To sum up, in this case, can I determine the equivalent capacity by the following?

$$C_{eq, x\to y}=\frac{q_1+q_4}{V_x-V_y}=\frac{q_3+q_5}{V_x-V_y}$$

And can I evaluate the charges I need (e.g. $q_1$ and $q_4$ ) by using mesh equations?

Yes. You'll have three mesh equations to deal with. Looking at the bridge, if you fix the potential x-y then you have two essential nodes and thus only two node equations. So maybe nodal analysis would be quicker. I fear the algebra will still get tedious.

Another approach altogether would be to apply a Y-Δ transformation on one of the suitable groupings of capacitors. Then brute force reduction of the network.

The ones I wrote in the question were intended to be mesh equations for the two loops (not including the one with the generator), plus generalized Ohm law for all the possible paths from $x$ to $y$: the sign of charges were assignet arbitrary for Ohm law (as showed in the picture the positive charge is always the one on the left face of capacitor). The choice of positive charges was respected in the two loop equation, orienting both loops clockwise and considering the sign of the charge firstly met on each capacitor while moving around the loop clockwise.

You could try assigning your charges in a similar fashion on the bridge version, then do a comparison with the original to see if they are consistent. Once again, how to assign the charge polarity on C2 will be problematical without knowing the actual values of all the components.