Volume of Solid Revolving Region About Line: 32pi/5

In summary, the formula for finding the volume of a solid revolving region about a line is V = ∫a^b π(R(x))^2 dx, where a and b are the limits of integration and R(x) is the distance from the line of rotation to the cross section at x. This is different from the volume of a solid of revolution, which is calculated by integrating along the circumference of the region. The line of rotation can be located anywhere in the region, but the formula for finding the volume will change depending on its location. The constant 32pi/5 represents the distance from the line of rotation to the cross section at x and is used in the formula to calculate the volume. This concept has real-world applications in
  • #1
windowsXLC
1
0
View attachment 8887

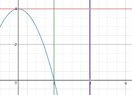
Find the region bounded above by the line y = 4, below by the curve y = 4 - x², and on the right by the line x = 2, about the line y = 4.

The Correct answer was: 32pi/5

I integrated from 0 to 2 of pi [(4)² - (4 - x²)²]

View attachment 8889

and got the answer of 224pi/15.

I tried every other possible ways and still didn't get the answer of 32pi/5.
 

Attachments

  • 1.jpg
    1.jpg
    14.9 KB · Views: 89
  • 11.jpg
    11.jpg
    1.9 KB · Views: 81
  • 11.jpg
    11.jpg
    2 KB · Views: 97
Physics news on Phys.org
  • #2
Your result would indeed be correct if you were revolving the bounded area about the \(x\)-axis, but you are to revolve the area about the line \(y=4\). Try that, and you'll get the required result. :)
 

FAQ: Volume of Solid Revolving Region About Line: 32pi/5

What is the formula for finding the volume of a solid revolving region about a line?

The formula for finding the volume of a solid revolving region about a line is V = π∫(R^2 - r^2)dx, where R is the outer radius, r is the inner radius, and dx represents the differential distance along the line of revolution.

How do you determine the outer and inner radii for calculating the volume?

The outer radius is the distance from the line of revolution to the outer edge of the solid region. The inner radius is the distance from the line of revolution to the inner edge of the solid region. Both radii can be determined by looking at the cross-sectional shape of the solid region.

Can the volume of a solid revolving region about a line be negative?

No, the volume of a solid region cannot be negative. It represents the amount of space occupied by the solid and is always a positive value.

What units are used for the volume of a solid revolving region about a line?

The units for the volume of a solid revolving region about a line will depend on the units used for the outer and inner radii. The volume will have units cubed, such as cm^3 or m^3.

Are there any real-world applications for calculating the volume of a solid revolving region about a line?

Yes, there are many real-world applications for calculating the volume of a solid revolving region about a line. For example, it can be used in engineering to determine the volume of a cylindrical tank or in architecture to calculate the volume of a dome-shaped structure.

Similar threads

MHB 18 Find the volume of the solid generated by revolving the region about y-axis.
Replies
4
Views
1K
B Why is this definite integral a single number?
Replies
20
Views
3K
MHB Triple Integrals: Finding Volume of Solid S Bounded by Planes
Replies
5
Views
2K
MHB What is the Volume of a Solid with Squares as Cross Sections?
Replies
2
Views
1K
MHB Find Volume of Revolved Region: [-pi/2, pi/2] & y= cos x & y = -cos x
Replies
5
Views
2K
MHB Calculate volume of a solid rotating around the y-axis
Replies
1
Views
2K
MHB How Do You Calculate Volume by Rotating a Region Bounded by Curves?
Replies
9
Views
2K
MHB Volume of Solid of Revolution; Simpson's Rule
Replies
1
Views
3K
Calculating the Volume of a Rotated Solid Using Calculus
Replies
6
Views
2K
MHB 8.2.2 Int area of a region and graph
Replies
1
Views
940

Hot Threads

Recent Insights

Back
Top