Waveguide: get I and II M.eq. from III and IV M.eq.

[crick]

Consider a waveguide with axis parallel to axis $z$. Using cartesian coordinates the fields inside the waveguide can be written as

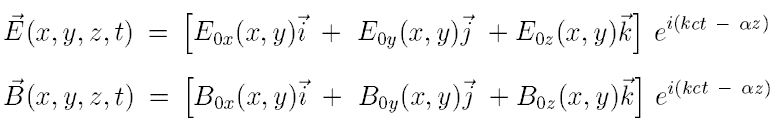
Where $\alpha$ is the wavenumber and $k=\frac{\omega}{c}$ .

The maxwell equations $\nabla \times E=-\frac{\partial B}{\partial t}$ and $\nabla \times B=\epsilon \mu \frac{\partial E}{\partial t}$ are written in components as

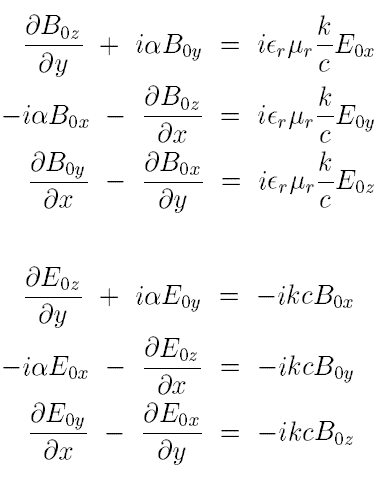$\tag{(A)}$While the maxwell equations $\nabla \cdot E=-\frac{\partial B}{\partial t}$ and $\nabla \cdot B=\epsilon \mu \frac{\partial E}{\partial t}$ are written in components as

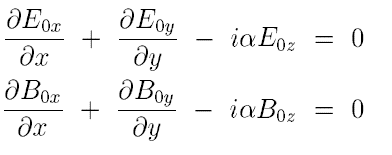
$\tag{(B)}$

On textboox it is claimed that equations $B$ are not useful, since they can obtained from equations $A$. So how to obtain equations $B$ using equations $A$?

 

[mjc123]

∇×E=−∂B/∂t

∇⋅E=−∂B/∂t

Are these both true? One should be a vector and one a scalar.

 

[vanhees71]

Of course, they are not true since
$$\vec{\nabla} \cdot \vec{E}=0, \quad \vec{\nabla} \cdot \vec{B}=0.$$
A vector can never ever be equal to a scalar!

 

[crick]

Are these both true? One should be a vector and one a scalar.

Of course, they are not true since
$$\vec{\nabla} \cdot \vec{E}=0, \quad \vec{\nabla} \cdot \vec{B}=0.$$
A vector can never ever be equal to a scalar!

EDIT OF THE QUESTION: I apologize, I made a mistake, I intended to write the first two maxwell equations, that are $\nabla \cdot E=0$ and $\nabla \cdot B=0$ (if there are no sources). $E$ and $B$ are intended to be vectors.