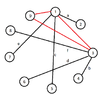
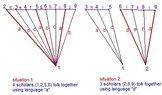
View attachment 7243
I use Alberts hint. Please cf. the attached diagram.
The conditions given are:
$(1).$ Each of the 9 scholars speaks at most three languages.
$(2).$ In a group of any three scholars, at least two scholars share a common language.
Graphical translation: Connecting scholars (dots) with language segments (lines).
According to condition $(1)$ each scholar on the diagram is allowed to have a maximum of three segments attached.
Condition $(2)$ implies, that no matter what group we form, there must be at least one interconnection (segment) in the group. (A group is e.g. $\{1,2,3\}$ meaning, that scholar no. $1$, $2$ and $3$ are in the group). There are $84$ possible groups, but we only need to consider some of them in order to prove the statement, that there are indeed at least three scholars, who share one common language.
In what follows, let´s suppose, that there are no three scholars sharing a common language.
Let´s start with scholar $1$:
Suppose scholar $1$ is connected with scholar $2$ by segment $a$, meaning that they can communicate in language $a$.
Obviously, there is no loss of generality by choosing a connection between scholar $1$ and $2$. But any new connection between two of the nine scholars from now on excludes language $a$, because any other “$a$-connection” would imply, that at least three scholars share the common language $a$.
All $7$ groups of the form $\{1,2,j\}$ with $3 \le j \le 9$ fulfill both conditions.Next, we look at the $6$ groups of the form $\{1,3,i\}$ where $4 \le i \le 9$. One of them is $\{1,3,4\}$. For this group to fulfill the requirements, we need at least one connection between two of the three members. We can WLOG connect $3$ and $4$ with segment $b$, that is: scholar $3$ and $4$ share a common language, which we call $b$.
(We could have connected $1$ and $4$ or $1$ and $3$. In both cases, we would need a new language $b$ and the end result of our procedure would be exactly the same).
The group $\{1,3,5\}$ doesn´t have any language connection. So either we connect $1$ and $5$ or $3$ and $5$ (or $1$ and $3$). In any of these cases this requires a new language ($c$). Let´s choose the connection $1$ to $5$.The same considerations for the group $\{1,3,6\}$: We need at least one connection. We choose, WLOG, $3$ and $6$ (language $d$).In $\{1,3,7\}$, we choose $1$ and $7$ with language $e$.In the group $\{1,3,8\}$, we have only one option left, because scholar $1$ already is occupied with $3$ languages ($a$,$c$,$e$).
So $3$ is connected with $8$ by language $f$, and scholar $3$ is then also occupied with $3$ languages ($b$,$d$,$f$).
But the group $\{1,3,9\}$ cannot fulfill the two conditions, because any single connection between two of the three scholars implies a fourth language segment, which is not allowed (red lines). Hence, we are forced to use one of the existing language segments e.g. $a$. This contradicts our assumption. Done.