JR Sauerland
Gold Member
- 44
- 0
I've highlighted the part in yellow I don't understand. He apparently 'drops' Δx in the last line, but doesn't display how. What I do know is that he is taking the limit as Δx→0, or as Delta x approaches zero. I'm simpy missing what he did though to drop the Δx. I mean, I understand he distributed x into the parentheses to get x0 squared, but not how he just dropped the Δx.
Any insight?
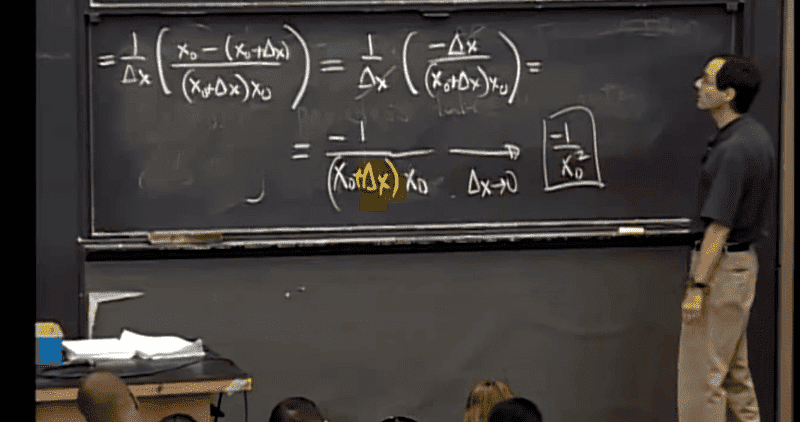
Any insight?