Although we normally ask that no more than 2 questions be asked per topic, and that effort be shown when posting questions, enough time has gone by that I am going to provide full solutions to the questions for the benefit of our readers.
3. Given a sphere with diameter 12 cm, find the surface area of the smallest cylinder containing the sphere.
The smallest cylinder that can contain a sphere of radius $r$ will have radius $r$ and height $h=2r$. And so the surface area $S$ of this cylinder is:
$$S=2\pi r^2+2\pi r(2r)=2\pi r^2\left(1+2 \right)=6\pi r^2$$
4. A rectangular box has sides of length 4 cm, 10 cm and 12 cm. What are the lengths of each of the four diagonals of the box?
There are 3 pairs of rectangular faces of the box, and to find the diagonal $d$ of a rectangle of base $b$ and height $h$, we may use the Pythagorean theorem as follows:
$$b^2+h^2=d^2\,\therefore\,d=\sqrt{b^2+h^2}$$
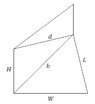
Now, for the diagonal of the entire box, consider the following diagram:
View attachment 1383
The box has the dimensions $L$, $W$ and $H$. As we can see the diagonal $d$ of the entire box is found from:
$$b^2+H^2=d^2$$
But, we see that:
$$b^2=L^2+W^2$$
Hence:
$$d=\sqrt{L^2+W^2+H^2}$$
And so the four diagonals of the box are:
$$d_1=\sqrt{L^2+W^2}$$
$$d_2=\sqrt{L^2+H^2}$$
$$d_3=\sqrt{W^2+H^2}$$
$$d_4=\sqrt{L^2+W^2+H^2}$$
Letting $L=4\text{ cm},\,W=10\text{ cm},\,H=12\text{ cm}$ we have:
$$d_1=\sqrt{4^2+10^2}=2\sqrt{29}\text{ cm}$$
$$d_2=\sqrt{4^2+12^2}=4\sqrt{10}\text{ cm}$$
$$d_3=\sqrt{10^2+12^2}=2\sqrt{61}\text{ cm}$$
$$d_4=\sqrt{4^2+10^2+12^2}=2\sqrt{65}\text{ cm}$$
5. A room measures 4 m by 7 m and the ceiling is 3 m high. A litre of paint covers 20 square metres. How many litres of paint will it take to paint all but the floor of the room?
We have two walls that are 4 m by 3 m, two walls that are 7 m by 3 m and the ceiling which is 4 m by 7 m, and so the total surface $S$ in square meters to be painted is:
$$S=2(4\cdot3+7\cdot3)+4\cdot7=94$$
To find the amount of paint $P$ in liters, we find:
$$P=\frac{1}{20}\frac{\text{l}}{\text{m}^2}\cdot94 \text{ m}^2=\frac{47}{10}\text{ l}=4.7\text{ l}$$
6. Find the dimensions of the smallest possible cubical box to hold a sphere of radius r. What percent of the volume will be air (percent nearest)?
The side lengths of the cubical box will have to be equal to twice the radius of the sphere, and so its volume is:
$$V_{\text{cube}}=(2r)^3=8r^3$$
The volume of the sphere is:
$$V_{\text{sphere}}=\frac{4}{3}\pi r^3$$
And so the portion of the box that is air is the volume of the box minus the volume of the sphere all divide by the volume of the box:
$$V_{\text{air}}=\frac{V_{\text{cube}}-V_{\text{sphere}}}{V_{\text{cube}}}=1-\frac{\frac{4}{3}\pi r^3}{8r^3}=1-\frac{\pi}{6}\approx48\%$$
7. The interior angles of an n-gon have an average measure of 175 degrees. Calculate n.
If we pick some central point within the polygon and draw radial line segments from this point to each of the $n$ vertices, then we have $n$ triangles the sum of whose interior angles is $n\cdot180^{\circ}$. If we then subtract the sum of the angles surrounding the central point, we then find that the sum $S$ of the interior angles of the $n$-gon is:
$$S=n\cdot180^{\circ}-360^{\circ}=(n-2)180^{\circ}$$
Now, if the interior angles of an $n$-gon have an average measure of $175^{\circ}$, then we know:
$$\frac{S}{n}=175^{\circ}\implies S=n\cdot175^{\circ}$$
And so, to find $n$, we may equate the two expressions for $S$:
$$(n-2)180^{\circ}=n\cdot175^{\circ}$$
Divide through by $5^{\circ}$:
$$36(n-2)=35n$$
Distribute on the left:
$$36n-72=35n$$
Add $72-35n$ to both sides:
$$n=72$$
Thus, the $n$-gon has 72 sides.