guyvsdcsniper
- 264
- 37
- Homework Statement
- Using Quick graph, plot a graph of acceleration vs. ∆m, using the Part I data. Based on your analysis of the graph, what is the relationship between the mass difference and the acceleration of an Atwood’s machine? Do a linear best fit, and report the slope value (don’t forget the units).
- Relevant Equations
- a=m/s^2
m=kg
I am doing an Atwood Simulation lab. I am having trouble with this part of my lab that ask the question provided.
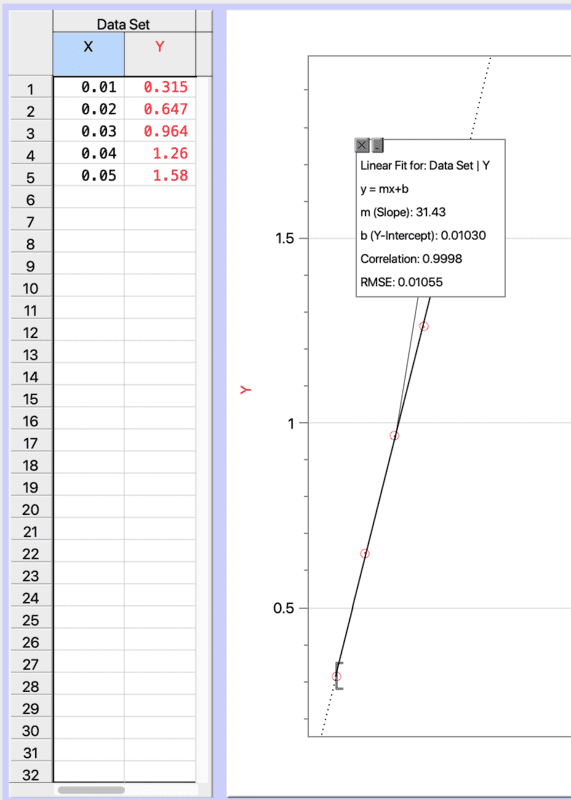
I can tell that the relationship is linear and that as the mass increases at a constant rate the acceleration increases.
Logger pro tells me that the slope is 31.43. I am having trouble thinking about what the units would be for the slope.
Acceleration is m/s^2. Mass is in kg. I believe that since I have a fraction of a kilogram I would then have:
m/s^2 / 1/kg which would then give me N.
Is that correct? If not where am I going wrong
I can tell that the relationship is linear and that as the mass increases at a constant rate the acceleration increases.
Logger pro tells me that the slope is 31.43. I am having trouble thinking about what the units would be for the slope.
Acceleration is m/s^2. Mass is in kg. I believe that since I have a fraction of a kilogram I would then have:
m/s^2 / 1/kg which would then give me N.
Is that correct? If not where am I going wrong
