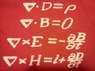Yeah, it's a little hard to read the symbols; let me write out the equations here.
\nabla \cdot D = \rho \\<br />
\nabla \cdot B = 0 \\<br />
\nabla \times E = -\frac{\partial B}{\partial t} \\<br />
\nabla \times H = i + \frac{\partial D}{\partial t}
The symbol \partial denotes partial differentiation--a derivative of a function of multiple variables that holds all others constant.
t is time. \rho here is the free charge density. We say "free" because charge can come from two sources; in particular, this charge density excludes charge that came from polarization of matter (where something that was neutrally charged gains positive charge in one place and negative in the other). Charge density that arises in this way is typically called "bound" charge.
i is the free current density, and there can be bound current density in the same way. Together, \rho and i are the "sources" of electromagnetic fields, E, D, B, H. E,D have to do with electric fields. E is usually called the electric field, while D is sometimes called the "electric displacement field". Usually, B is called the magnetic field nowadays, whereas H has a few different names, but it's often just referred to by its symbol as "the H-field".
E,B,D,H are vector fields, and the \nabla \cdot and \nabla \times describe how the derivatives of these fields must relate to the sources or to other time derivatives of fields.
This image appears to be in a specific set of units; often, you might see Maxwell's equations in SI units instead, and you'll see constant factors of \epsilon_0,\mu_0 in places. These just make the numbers work. Finally, you might see Maxwell's equations in vacuum, which simplify things considerably: without matter that can be polarized, D and H basically reduce to E and B respectively. There are also integral forms of Maxwell's equations, which are generated through a nifty piece of mathematics called Stokes' theorem, but they say the same thing.
That's the 30-second explanation of Maxwell's equations in a nutshell; wikipedia would do a far better job of explaining them than I ever could. The classical theory of electromagnetism is one of the most fascinating aspects of physics, and there's quite a bit of history to it that has helped shape our understanding not only of light but of space and time. Maxwell's equations predict that the speed of light is constant regardless of one's speed, and that helped motivate the theory of relativity. It is a robust, elegant theory and worthy of many hours of study, in my opinion.