meanswing
- 10
- 0
Hi Everyone. I am trying to find out when this paddle (in red) would break due to the force of the drag of the water and from the force of the pneumatic cylinder that is pushing it. I took intro to statics but as you can see with the figure the machine is not static. Can someone point me to the right direction.
______________________________________________________________________________
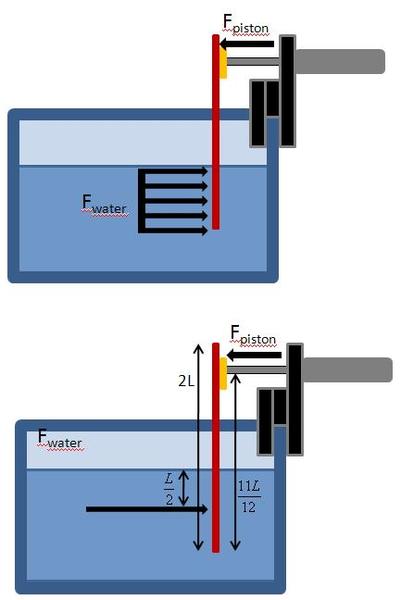
Here is my attempt:
let the force of the water be the drag force of the water, F_w = C_d*rho*v^2*A_p , where C_d is the coefficient of drag of the paddle, rho is the density of water, v is the velocity of the paddel, and A_p is the cross sectional area of the paddle exposed to the water. The force of the pneumatic piston is, F_p = P*A_b = P*pi*d^2/4 , such that P is the pressure supplied to the cylinder and d is the diameter of the piston bore.
The paddle will break when the applied forces exceeds the paddles yield strength so. Let sigma be the yield strength resulting from the drag force and the force of the piston.
sigma = (F_w + F_p)/A_p
______________________________________________________________________________
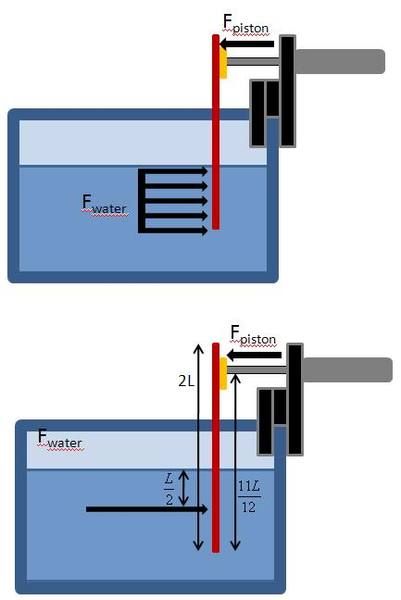
Here is my attempt:
let the force of the water be the drag force of the water, F_w = C_d*rho*v^2*A_p , where C_d is the coefficient of drag of the paddle, rho is the density of water, v is the velocity of the paddel, and A_p is the cross sectional area of the paddle exposed to the water. The force of the pneumatic piston is, F_p = P*A_b = P*pi*d^2/4 , such that P is the pressure supplied to the cylinder and d is the diameter of the piston bore.
The paddle will break when the applied forces exceeds the paddles yield strength so. Let sigma be the yield strength resulting from the drag force and the force of the piston.
sigma = (F_w + F_p)/A_p