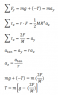Daisy Muller
- 1
- 0
1. Homework Statement
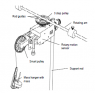
In each question: you place mass m on the mass holder, and released the system from rest. The system includes the long rod with two point masses on it (see the picture next to the list of equipment).
Since this is a rotational and translational motion, I set up two equations: sum of the force and torque
unknown will be angular acceleration and moment of inertia.
Homework Equations
The Attempt at a Solution
Sorry. I guess I put my solution in the above.
a)
if you increase m, the mass on the mass holder, what happens to the following quantities:
- α, the angular acceleration of the pulley.
- I, the moment of inertia of the pulleys-plus-rod system.
The change of mass in the holder won't affect either of them. Therefore, they remain unchanged. Although I tempt to follow other opinions on web, adding extra weight will increase the velocity. But somehow Galileo keeps popping up in my head.
b)
you wrap the string around the smallest radius wheel in the "3-step pulley" (see diagram). If you wrap the string around a greater radius wheel, using the same mass on the mass holder, what will happen to the following quantitiesA:
- α, the angular acceleration of the pulley.
- I, the moment of inertia of the pulleys-plus-rod system.
Increase the radius will make angular acceleration smaller; therefore, angular acceleration will be decreased. Here is something I don't understand. I don't see the I= moment of inertia in the final equation and I tempted to go back to rotational motion and use it to interpret it. But I know something's wrong. Because it doesn't include in the final solution. Sorry. If I keep repeating myself, hopefully it'll not confuse you.
Therefore, I propose the moment of inertia remains unchanged even the radius is increased.
c)
if you move the two masses attached to the rotating rod away from the center of mass of the rod, what happens to the following quantities:
- α, the angular acceleration of the pulley.
- I, the moment of inertia of the pulleys-plus-rod system.
I don't know what I think of the last part. There is another system on top of the disk. It means another radius and new mass introduce into the system. I did this lab already. I remember it didn't affect the result. But I don't want to rely on memory. Can you shed some light on it? Daisy