Discussion Overview
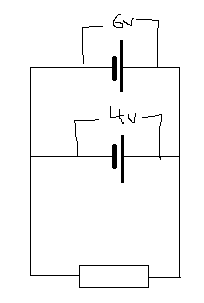
The discussion revolves around the hypothetical scenario of connecting a 6V battery and a 4V battery in parallel, both assumed to have negligible internal resistance, along with resistors. Participants explore the implications of applying Kirchhoff's laws in this context and the contradictions that arise from such a configuration.
Discussion Character
- Debate/contested
- Technical explanation
- Conceptual clarification
Main Points Raised
- One participant expresses confusion about determining the potential difference across the resistor in the circuit due to contradictory answers when applying Kirchhoff's voltage rule.
- Another participant suggests that the assumptions of circuit theory break down in this scenario, indicating that the presence of impedance in the cells or wires must be considered.
- A third participant agrees that the scenario leads to contradictions and emphasizes that valid circuit analysis should not yield infinite voltages or currents.
- Further, it is noted that the circuit definition inherently contains a contradiction related to Kirchhoff's voltage law, necessitating the specification of internal resistances before analysis.
- One participant elaborates on the limitations of Kirchhoff's laws, stating that they are applicable only to ideal components and that real-world components may require more complex modeling to avoid nonsensical scenarios.
- Additionally, the discussion touches on the existence of impossible scenarios in network theory, particularly those involving only voltage sources or current sources, highlighting the complexity of circuit analysis.
Areas of Agreement / Disagreement
Participants generally agree that the scenario presents contradictions and that Kirchhoff's laws may not apply straightforwardly. However, there is no consensus on how to resolve these contradictions or the implications for circuit analysis.
Contextual Notes
Participants note that the discussion is limited by the assumptions made about ideal components and the necessity of including internal resistances in the analysis. The implications of using idealized models versus real-world components remain unresolved.