mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
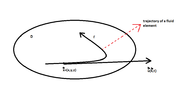
Let the fluid occupies the space $D \subset \mathbb{R}^n, n=2 \text{ or } 3$.
$\overrightarrow{x}$ is a point of $D$.
We consider the element of the fluid that is at the position $\overrightarrow{x}$ at the time $t$ , and moves along the trajectory $\Gamma$.
View attachment 4404
Let $\overrightarrow{u}(\overrightarrow{x}, t)$ the velocity of this element. For a given time $t$, $\overrightarrow{u}(\cdot , t)$ is a vector field over $D$, and is called velocity field.
Could you explain to me the last part:
"For a given time $t$, $\overrightarrow{u}(\cdot , t)$ is a vector field over $D$, and is called velocity field."
?? (Wondering)
Let the fluid occupies the space $D \subset \mathbb{R}^n, n=2 \text{ or } 3$.
$\overrightarrow{x}$ is a point of $D$.
We consider the element of the fluid that is at the position $\overrightarrow{x}$ at the time $t$ , and moves along the trajectory $\Gamma$.
View attachment 4404
Let $\overrightarrow{u}(\overrightarrow{x}, t)$ the velocity of this element. For a given time $t$, $\overrightarrow{u}(\cdot , t)$ is a vector field over $D$, and is called velocity field.
Could you explain to me the last part:
"For a given time $t$, $\overrightarrow{u}(\cdot , t)$ is a vector field over $D$, and is called velocity field."
?? (Wondering)