What is the angle between star A, B, and C on the celestial sphere?

[tony873004]

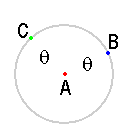
Let's say I have 3 lasers: A B and C. They are all at the same location in a room representing a 3D grid. I shine laser A at the wall, but not necessarily perpendicular to the wall. I shine laser B at the wall so that its beam forms the angle AB. I then shine laser C at the wall forming angle AC. Angle AC =AB, although B doesn't fall on the same spot on the wall as C. They both fall on a lotus of points forming a circle around point A since their angles from A are equal. I carefully measure the x, y, and z compoients of all 4 points:
P1: lasers' position
P2: beam A strikes the wall
P3: beam B strikes the wall
P4: beam C strikes the wall

I can find the angle AB with
arcos (A dot B) / (|A| |B|)
where A is the vector joining P1 and P2, and B is the vector joining P1 and P3.

And I can find the angle AC with the same method. These two angles equal each other. But how do I determine the angle of the arc between B and C on the lotus of points that surround point A?

 

[micromass]

Hi tony873004!

Let me get things straight so I know for certain that we'll be talking about the same thing.

This is the picture of your wall, right? And the red dot is where A hits the wall and it is what you called P1. The blue dot is P2 and the green dot is C3?

Now, you're interested in the angle between the lines formed by the lines (green dot, red dot), (blue dot, red dot). That is, the angle that the dots make on the wall??

Am I getting this right?

 

[HallsofIvy]

I presume that your picture shows the way where the lasers hit the wall. Exactly what information can you use? If all you know are angles AB and AC there is no way to determine the angle between B and C. Points B and C could be any points on that circle.

 

[Studiot]

Not sure about this exercise in 3D geometry.

You say that angle AC = BC.
Is this a typo? Do you mean Angle AC = Angle AB ?

Later you say that you find angles AB and AC and that they are equal.

P2, P3 & P4 are coplanar, so if you know the coordinates of all three by measurement surely you can solve the triangle to yield angle P3P2P4 and the circle radius

The arc between P3 and P4 will be the radius times this angle.

 

[tony873004]

You say that angle AC = BC.
Is this a typo? Do you mean Angle AC = Angle AB ?

Yes, that was a typo. AC=AB

 

[Studiot]

I carefully measure the x, y, and z compoients of all 4 points:

Then the rest of my post completes the answer.

However since three of the points of interest are on the wall you only need take measurements on the wall of the distances between the three points. That is enough to solve the triangle. Do you need assistance with that?

 

[tony873004]

Hi tony873004!

Let me get things straight so I know for certain that we'll be talking about the same thing.



This is the picture of your wall, right? And the red dot is where A hits the wall and it is what you called P1. The blue dot is P2 and the green dot is C3?

Now, you're interested in the angle between the lines formed by the lines (green dot, red dot), (blue dot, red dot). That is, the angle that the dots make on the wall??

Am I getting this right?

Yes, it's a picture of the wall. What is not shown here is P1, the position of the lasers, which would be where you, the viewer is. What I know how to determine is the angle between the vector that connects the viewer and point A, and the vector that connects the viewer and point B. Same for A and C. I want to know how to determine the angle of the arc that connects points B and C, which in my diagram appear to be about 90 degrees apart.

 

[micromass]

Let $(x_n,y_n,z_n)$ be the coordinate of the point P_n.

The vector connecting point A and point B is the same as the vector connecting (0,0,0) with $(x_3-x_2,y_3-y_2,z_3-z_2)$. The vector connecting A anc C is the same as the vector connecting (0,0,0) and $(x_4-x_2,y_4-y_2,z_4-z_2)$.

So all you have to do now is find the angle between the vectors$(x_3-x_2,y_3-y_2,z_3-z_2)$ and $(x_4-x_2,y_4-y_2,z_4-z_2)$. This can be done by taking the inproduct.

Could this be what you're looking for? Or did I see things completely wrong?

 

[tony873004]

I don't think I phrased my question very well :(. Let me try again.
A viewer on Earth sees a star in the sky. Call it star A. Surrounding this star is a circle representing all angular distances 5 degrees from the star. Two more stars, stars B and C lie on this circle.

The (x,y,z) positions of Earth and the 3 stars are known.
Vector A connects Earth to star A.
Vector B connects Earth to star B.
Vector C connects Earth to star C.

acos(A dot B / (|A| |B|)) = 5 degrees, and
acos(A dot C / (|A| |C|)) = 5 degrees.

Is there any way to determine how many degrees separate stars B and C along the circle that joins them?

 

[Studiot]

A viewer on Earth sees a star in the sky. Call it star A. Surrounding this star is a circle representing all angular distances 5 degrees from the star. Two more stars, stars B and C lie on this circle.

This is not the same as points on a flat wall.

You are now talking about a circle on the surface of a (celestial) sphere and spherical trigonometry, for which the formulae are different.

 

[tony873004]

This is not the same as points on a flat wall.

You are now talking about a circle on the surface of a (celestial) sphere and spherical trigonometry, for which the formulae are different.

I realized that when my laser A didn't hit the wall perpendicularly, but I still drew a circle around it. On the wall this would be an ellipse.

What I'd like to do is plot an image of these 3 stars viewed from Earth, with star A in the middle of the image, star B at an arbitrary point along the circle, and star C at the proper position relative to star B on the circle.