Ellipse of transformation from spherical to cartesian

[octopode]

Hi,

I have to resample images taken from camera, whose target is a spherical object, onto a regular grid of 2 spherical coordinates: the polar and azimutal angles (θ, Φ). For best accuracy, I need to be aware of, and visualise, the "footprints" of the small angle differences onto the original images, so I tried to represent the ellipses of transformation at 3 different positions, which in the output space (θ, Φ) are at p1=(0, 0), p2=(0, 60) and p3=(30, 0). I tried using a linearization with the Jacobian matrix but I am not sure I did it right, or if that's enough.
First, consider my screenshot:

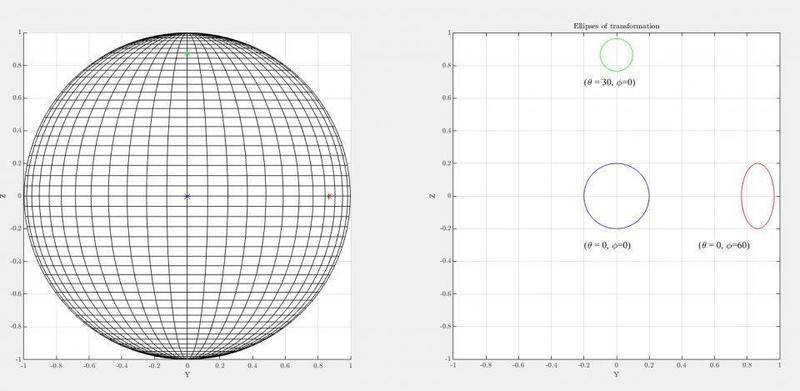
It shows (left) the spherical grid with a unit-sphere, with the three points p1, p2, p3 that I consider. On the right-hand side, we have my ellipses of transformation, which I interpret as the footprint onto the input space (the original image coordinates ) from small angle differences in the input space. While I expected the shape of the blue and red ellipse as they are here, I do not understand why the green one is not the 90-degrees-rotated red circle. Instead it is just a smaller circle. The original image is taken from a viewpoint in the X-axis, using the present coordinate space and X-, Y-,Z- axis of the left-hand side figure.

I used this formula for the Jacobian of the transformation from Spherical to Cartesian coordinates for the unit-sphere:

$\textbf{J} = \begin{pmatrix} \sin(\theta)\cos(\phi) & \cos(\theta)\cos(\phi) & -\sin(\theta)\sin(\phi) \\ \sin(\theta)\sin(\phi) & \cos(\theta)\sin(\phi) & \sin(\theta)\cos(\phi) \\ \cos(\theta) & -\sin(\theta) & 0 \end{pmatrix}$

associated with the following transformation from spherical to cartesian (with a unit radius):

$x = \sin(\theta) \cos(\phi) \\ y = \sin(\theta) \sin(\phi) \\ z = \cos(\theta)$

Then the ellipses of transformation are obtained by multiplying J by a vector of coordinate (dθ, dΦ) that satisfies the equation of a circle of a radius smaller than 1 (0.2 in this example) so I can see the footprints in all direction.

Am I missing something obvious ?

Thanks

 

[andrewkirk]

Hello octopode.

Why are you using a Jacobian? It looks like what you are aiming to do is plot the y and z coordinates of points in three circles of radius 0.2, centred at each of the the three points. If you parametrise the circumference of such a circle $C_n$ around point $p_n$, with starting point $q_n$ on the circumference, by function $f_n:[0,2\pi]\to\mathbb{R}$ and $g_n:[0,2\pi]\to\mathbb{R}$ such that $f_n(t)$ and $g_n(t)$ are respectively the $\theta$ and $\phi$ coordinates of the point that has traveled angle $t$ around $C_n$ from $q_n$, then all you need to do is use your conversion formulas:
$$x = \sin(\theta) \cos(\phi) \\ y = \sin(\theta) \sin(\phi) \\ z = \cos(\theta)$$
to get the y and z coordinates of that path, and plot them on a y-z number plane.

Also, I noticed that your coordinates of p3=(30,0) do not match the green mark you have made on your ellipse. The green mark looks more like around (75,0). The angle of elevation is well above 45 degrees, and certainly not 30. I don't know if that reflects a problem in the calcs or just putting the mark in the wrong place.

 

[octopode]

Hello Andrewkirk,

Thank you for this first reply. First of all, as I described, θ is the polar angle, not elevation. So it's 90 degrees minus the "elevation". The polar angle is 0 on the Z-axis. Otherwise, we wouldn't have z = cos(θ) but z = sin(θ) and the whole formula would be different.

As for parametrising Cn , using directly the conversion formula, I don't see how different that makes things . The advantage of the Jacobian is that once applied to a circle like I did, by property, it transforms it into an ellipse of transformation. And a straight look at the Jacobian gives instantly the major and minor axes changes on the ellipse. Nonetheless, I will also try your approach to make sure I also look at this problem from your vantage point.

However, I realize that my ellipses of transformation may be correct. The choice of re-mapping using a regular grid of θ and φ and make z varies as a function of θ, but y varies also as a function of (φ) and that makes the Jacobian at (30, 0) diagonal with equal elements on the diagonal , while it is not the case at (0, 60), resulting in just a linear scaling of the ellipse axes on the z axis at (30, 0) (so the blue circle shrinks into this green circle as we go up on the z-axis), while reshaping the circle in an ellipse at (0, 60). In that sense, the ellipses I see are consistent with the Jacobian calculation.

 

[andrewkirk]

θ is the polar angle, not elevation. So it's 90 degrees minus the "elevation". The polar angle is 0 on the Z-axis.

With that definition, the points p1=(0,0) and p2=(0,60) are the same point, which is the North Pole of the sphere. Yet none of the three points marked on the diagram are at either pole of the sphere. The latitudes of the two marked points on the equator agree with an interpretation of $\theta$ as elevation, but not as polar angle.

Also, I have a question about your terminology: what do you mean by 'ellipse of transformation'? Google doesn't seem to have heard of it. 'Transformed ellipses' (under a wide variety of different types of transformations) yes, but not 'ellipse of transformation'.

 

[octopode]

With that definition, the points p1=(0,0) and p2=(0,60) are the same point, which is the North Pole of the sphere. Yet none of the three points marked on the diagram are at either pole of the sphere. The latitudes of the two marked points on the equator agree with an interpretation of $\theta$ as elevation, but not as polar angle.

Also, I have a question about your terminology: what do you mean by 'ellipse of transformation'? Google doesn't seem to have heard of it. 'Transformed ellipses' (under a wide variety of different types of transformations) yes, but not 'ellipse of transformation'.

You are totally right for p1, it's a mistake. It should read p1 = (90, 0), p2 = (90, 60), p3 = (30, 0), which is what all my code is using. I was using "elevation" angles instead of polar angles a few days ago and it got stuck in my head. I'll update it in the first post.

Regarding the terminology for "ellipse of transformation". I see it on some math courses and publications my work is based on, about image resampling (restricted access unfortunately). It's the same as "transformed ellipse" that you see on google, and I use it in the same sense as in the graphical illustration of Singular Value Decomposition (SVD).

[Update] I can't edit my first post. So, I meant the 3 points at p1 = (90, 0); p2 = (90, 60); p3 = (30, 0)

 

[octopode]

Here is a new screenshot with corrected points (calculations and codes were already using this).

 

[andrewkirk]

Right, those points now look good. All that part makes sense. Whether the diagram on the right is correct depends on what the pre-transformation shape is. The shapes for p1 and p2 look roughly OK regardless. But for p3 it depends. If the pre-transformation shape is a circle drawn on the sphere - ie the set of all points that are great-circle distance 0.2 from p3 - then the post-transformation shape will be roughly similar to an ellipse with the major axis horizontal. So the shape shown is wrong.

On the other hand, if the pre-transformation shape is something like the set of all points $q$ with coordinates $(\theta(q),\phi(q))$ such that $\sqrt{(\theta(q)-\theta(p3))^2+(\phi(q)-\phi(p3))^2}=0.2$ then that shape will be roughly elliptical with the major axis pointing towards the North Pole, so when viewed from the chosen vantage point it could well look roughly circular as shown.

Which of those is correct for your purpose depends on what that purpose is. I think for most purposes the first would be correct, in which case the calculation is incorrect, as it looks like it's taking the second approach.

I would also point out that, if the shapes drawn above are perfect ellipses using axis lengths transformed by the Jacobian, then they will not be exactly correct for the second interpretation either, as the true footprints of the shapes on the Y-Z grid are not perfect ellipses. The linearised approach assumes there is no curvature of the sphere within the drawn shape. That approaches perfect accuracy as the size of the shape shrinks to a point. For a very small shape the linearised approach may be reasonable but for circles of the size drawn it will be fairly inaccurate.

 

[octopode]

On the other hand, if the pre-transformation shape is something like the set of all points qqq with coordinates $(θ(q),ϕ(q))(θ(q),ϕ(q))(\theta(q),\phi(q))$ such that $√(θ(q)−θ(p3))2+(ϕ(q)−ϕ(p3))2=0.2(θ(q)−θ(p3))2+(ϕ(q)−ϕ(p3))2=0.2\sqrt{(\theta(q)-\theta(p3))^2+(\phi(q)-\phi(p3))^2}=0.2$ then that shape will be roughly elliptical with the major axis pointing towards the North Pole, so when viewed from the chosen vantage point it could well look roughly circular as shown.

I'm using this above method.

For a very small shape the linearised approach may be reasonable but for circles of the size drawn it will be fairly inaccurate.

I agree. I exaggerated the radius on purpose, so we can see something. But I realize it's not very consistent with using the Jacobian method, as linearization only applies in the "vicinity" of a given point p. Yet I'm going rather far away from it.

In practice, the input space would be a pair (x, y) of coordinates of pixels in a 2048 x 2048 image. And the variation in the output space ( θ and φ) between one grid point to the next should cover 1 pixel or less. So, for the Jacobian method to work, I would use a radius of much less than one degree and much less than 0.2 given that 1 pixel, in my case, covers, in fact, a few arcsec...

Nonetheless, you're right, if I use the linearization method with the Jacobian in the present example, I should stick to values << 1, and then compare with your approach.

 

[octopode]

So, just to make things more rigorous (I hope...), here is an updated screenshot. For the small ellipses I use dθ and dφ spanning no more than 0.02 (so, they vary between -0.01 and +0.01). That makes the circle in input space (θ, φ) that multiplies the Jacobian, and on top of that I put the bigger ellipses that just magnifies both ellipses axes by 20 to have an anamorphosis that emulates a local "x20 zoom".