What is the angle of NMC in triangle ABC with given measurements?

[anemone]

In the triangle ABC, we have $\angle ABC=100^\circ$, $\angle ACB=65^\circ$, $M\in AB$, $N\in AC$, $\angle MCB=55^\circ$ and $\angle NBC=80^\circ$. Find $\angle NMC$.

 

[Albert1]

In the triangle ABC, we have $\angle ABC=100^\circ$, $\angle ACB=65^\circ$, $M\in AB$, $N\in AC$, $\angle MCB=55^\circ$ and $\angle NBC=80^\circ$. Find $\angle NMC$.

$ \angle A=15^o$

using MC as a mirror we got triangle A' MC as a symetric image of triangle AMC

then it is very easy to see that :

$ \angle NMC=25^o=\angle A+(65^o - 55^o)$

 

[anemone]

$ \angle A=15^o$

using MC as a mirror we got triangle A' MC as a symetric image of triangle AMC

then it is very easy to see that :

$ \angle NMC=25^o=\angle A+(65^o - 55^o)$

Hi Albert, I want to thank you for participating in this problem but your answer doesn't match mine.

Here is my solution:
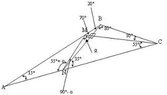
View attachment 697

First I let the angle NMC be $$\alpha$$.
Consider the triangle NPM,
$$\sin \alpha=\dfrac{NP}{MN}$$

Consider the triangle NCP,
$$\sin 55^{\circ}=\dfrac{NP}{CN}$$

$$\therefore NP=CN\sin 55^{\circ}$$

Now, since NP can be expressed as the function of CN, I will figure out a way to express MN in terms of CN because that is one of the valid method to find the measure of the angle $$\alpha$$.

Consider the triangle AMN,
$$\dfrac{MN}{\sin 15^{\circ}}=\dfrac{AM}{\sin (55+\alpha)^{\circ}}\implies$$ $$MN=\dfrac{AM\sin 15^{\circ}}{\sin (55+\alpha)^{\circ}}$$

But $$\dfrac{AM}{\sin 55^{\circ}}=\dfrac{CM}{\sin 15^{\circ}}$$ (from the triangle AMC)

and $$\dfrac{CM}{\sin 100^{\circ}}=\dfrac{BC}{\sin 70^{\circ}}$$ (from the triangle CMB)

Thus,

$$AM=\dfrac{CM\sin 55^{\circ}}{\sin 15^{\circ}}=\dfrac{BC\sin 100^{\circ}}{\sin 70^{\circ}}\cdot\dfrac{\sin 55^{\circ}}{\sin 15^{\circ}}$$ but $$\dfrac{BC}{\sin 35^{\circ}}=\dfrac{CN}{\sin 80^{\circ}}$$ (from the triangle BCN)

$$\therefore AM=\dfrac{CN\sin 35^{\circ}}{\sin 80^{\circ}}\cdot\dfrac{\sin 100^{\circ}}{\sin 70^{\circ}}\cdot\dfrac{\sin 55^{\circ}}{\sin 15^{\circ}}$$

or

$$MN=\dfrac{\sin 15^{\circ}\dfrac{CN\sin 35^{\circ}}{\sin 80^{\circ}}\cdot\dfrac{\sin 100^{\circ}}{\sin 70^{\circ}}\cdot\dfrac{\sin 55^{\circ}}{\sin 15^{\circ}}}{\sin (55+\alpha)^{\circ}}$$

We have now:
$$\sin \alpha=\dfrac{NP}{MN}$$

$$\sin \alpha=\dfrac{CN\sin 55^{\circ}}{\dfrac{\sin 15^{\circ}\dfrac{CN\sin 35^{\circ}}{\sin 80^{\circ}}\cdot\dfrac{\sin 100^{\circ}}{\sin 70^{\circ}}\cdot\dfrac{\sin 55^{\circ}}{\sin 15^{\circ}}}{\sin (55+\alpha)^{\circ}}}$$

Simplifying the above yields

$$\sin \alpha=2\cos35^{\circ}\sin (55+\alpha)^{\circ}$$

This gives$$\tan \alpha=\dfrac{2\cos35^{\circ}\sin55^{\circ}}{1-2\cos35^{\circ}\sin55^{\circ}}$$

Finally, we get $$\angle NMC=\alpha=87.4270^{\circ}$$

So Albert, who is right and who is wrong?

BTW, may I look at your diagram because I have a little hard time trying to figure out your solution, please?

Thanks.

 

[Albert1]

anemone:
Your diagram is not correct ,please check it

note :angle MCB=$55^o$,
but your diagram angle MCB=$10^o$
do it again ,I will post my solution later

 

[anemone]

anemone:
Your diagram is not correct ,please check it

note :angle MCB=$55^o$,
but your diagram angle MCB=$10^o$
do it again ,I will post my solution later

Yes, you're right, I labeled the angle incorrectly and by redoing the problem, I found that $$\angle NMB=25^{\circ}$$.

Your approach must be one of the smartest one because you solved it by observation but I approached it using lots of messy equations and therefore, my hat is off to you, Albert!(Wink)

 

[I like Serena]

Your approach must be one of the smartest one because you solved it by observation but I approached it using lots of messy equations and therefore, my hat is off to you, Albert!

Ah, but you don't know how much paper and messy equations he spent before giving a short answer. ;)

 

[Albert1]

yes before giving a short and smart solution ,I racked my brain,and spent much time thinking :)
View attachment 698

 

[Petrus]

Maybe off topic but what does exemple $\angle ABC=100^\circ$ means?

 

[I like Serena]

Maybe off topic but what does exemple $\angle ABC=100^\circ$ means?

It's the angle at point B between the sides AB and BC.
To be honest, I was puzzling myself which angle was intended exactly, but looking at the other angles, I deduced that this is what was intended.

 

[MarkFL]

Maybe off topic but what does exemple $\angle ABC=100^\circ$ means?

Asking for clarification about a step taken or notation used is encouraged, as this is how we learn, and is not considered off-topic at all. :D