SUMMARY
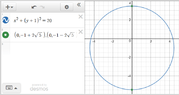
The discussion focuses on determining the center and radius of a circle, as well as finding the y-coordinates of intersection points with the y-axis. The equation used is \(x^2 + (y + 1)^2 = 20\), confirming that if the circle intersects the y-axis, the x-coordinate is 0. The y-coordinates of intersection points are calculated as \(y = -1 \pm 2\sqrt{5}\), resulting in the points \((0, -1 + 2\sqrt{5})\) and \((0, -1 - 2\sqrt{5})\).
PREREQUISITES
- Understanding of circle equations in the form \((x-h)^2 + (y-k)^2 = r^2
- Knowledge of algebraic manipulation and solving equations
- Familiarity with square roots and their properties
- Basic coordinate geometry concepts
NEXT STEPS
- Learn how to derive the center and radius from the standard form of a circle equation
- Study the implications of circle intersections with coordinate axes
- Explore the use of the quadratic formula in solving for y-coordinates
- Investigate the geometric interpretations of circle equations and their graphs
USEFUL FOR
Students, educators, and anyone interested in mastering the concepts of circle geometry and algebraic equations related to conic sections.