What is the difference between static friction and rolling resistance?

[googly_eyes]

Hi, it's probably a frequent question, but I can't seem to wrap my hear around. I'm trying to understand how I reach that value, not just how to get the value.
I'm designing a vehicle with 4 wheels. It'll climb a surface with a slope theta (in degrees).
This is the FBD that I've come up with of a wheel. Following my analysis, the torque M that the motor needs to provide is simply Fr*R, where Fr is the friction force.

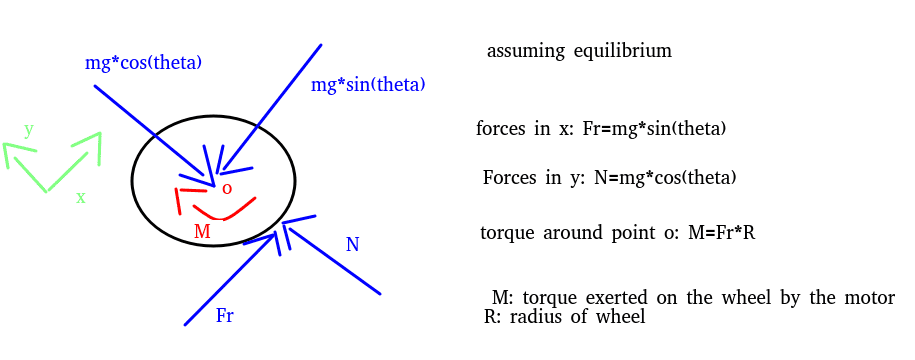
However, I've seen docs on the internet (page 35/60) that instead considers that the required torque includes an extra force (let's forget about the acceleration and wind force), which is mg*sin(theta)*R. This completely changes the torque analysis, and I don't know why it's like that (not explanation/analysis is given, just that). And I've seen the same equation on other places, including this extra member to the equation force. But alas, I'm clueless as to why it's like that. If you could please enlighten me, an explanation/FBD, whatever fits you, to explain this to me.
Many thanks

 

[Keith_McClary]

If you had a rack railway which can't slip at all (infinite friction?) then you would only have the mg*sin(theta)*R term.
The friction force term corresponds to the maximum torque without slipping.

 

[googly_eyes]

If you had a rack railway which can't slip at all (infinite friction?) then you would only have the mg*sin(theta)*R term.

I'm sorry, I fail to see how that term appears if you take momentum with respect to the center of mass.

The friction force term corresponds to the maximum torque without slipping.

The worst case scenario, correct?

 

[Dullard]

Your 'Fr*R' and 'mg*sin(theta)*R ' are the same (as you define Fr). The paper that you cited defines Fr as 'rolling resistance' - that's a dynamic force - not relevant in a static analysis.

I would call your Fr the 'traction' (not 'friction') force.

 

[googly_eyes]

Your 'Fr*R' and 'mg*sin(theta)*R ' are the same (as you define Fr). The paper that you cited defines Fr as 'rolling resistance' - that's a dynamic force - not relevant in a static analysis.

I would call your Fr the 'traction' (not 'friction') force.

Now that you mention it, that's true. But for example, in this page make an analysis and turns out that M=mg*(sinθ+cosθ*μr)*R - the maximum static friction is added. This analysis only considers forces, and then derives the motor torque. Shouldn't I reach the same result?

And you can also find this similar equation in this online calculator. They consider other factors such as number of wheels (n1) and the weight of each wheel (md1), but it's basically the total mass of the system. The other term doesn't matter because it's all zero, so it doesn't affect.

 

[Dullard]

You're confusing static friction and rolling resistance. Static friction is what keeps the tire from slipping. As long as it is not exceeded, it doesn't matter to your calculations. 'Rolling friction' is (mostly) the effort wasted into changing the shape of the tire as it rolls. Rolling friction is not relevant to a static analysis (which is what you appear to be attempting).