- #1
chessguy103
- 13
- 3
Hi everyone,
I'm working on designing a vehicle that uses electric motors, but I'm having a little trouble finding the load and acceleration torques in order to select the right motors to use.
Variables:
m = total mass of vehicle
a = acceleration
μ_r = rolling friction coefficient
r = wheel radius
N = normal force (vehicle weight)
J = moment of inertia
F_r = rolling friction
T_L = load torque
T_a = acceleration torque
α = angular acceleration
Assumptions:
Calculations:
Here's what I've calculated so far. If I've made any mistakes or left anything out, please correct me.
Load torque:
Acceleration torque:
I tried calculating this in two ways and got two different answers.
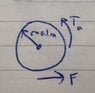
1. First I used a free body diagram, attached below.
2. Here's where I'm getting confused.
Any help is appreciated. Thanks :)
I'm working on designing a vehicle that uses electric motors, but I'm having a little trouble finding the load and acceleration torques in order to select the right motors to use.
Variables:
m = total mass of vehicle
a = acceleration
μ_r = rolling friction coefficient
r = wheel radius
N = normal force (vehicle weight)
J = moment of inertia
F_r = rolling friction
T_L = load torque
T_a = acceleration torque
α = angular acceleration
Assumptions:
- m = 50 kg (distributed evenly across 4 wheels)
- a = 2 m/s^2
- μ_r = 0.02
- r = 0.1 m
- Vehicle driven by two back wheels using two separate electric motors (direct drive)
- Driving on a flat surface
Calculations:
Here's what I've calculated so far. If I've made any mistakes or left anything out, please correct me.
Load torque:
- F_r = μ_r * N
- N = 50 kg * 9.81 m/s^2 = 490.5 N
- F_r = 0.02 * 490.5 N = 9.81 N
- T_L = F_r * r
- T_L = 9.81 N * 0.1 m = 0.981 Nm
Acceleration torque:
I tried calculating this in two ways and got two different answers.
1. First I used a free body diagram, attached below.
- F = ma = 50 kg * 2 m/s^2 = 100 N
- 2 Driving wheels --> 2T = Fd = 100 N*0.1 m = 10 Nm
- T = 5 Nm (per driving wheel)
2. Here's where I'm getting confused.
- T_a = J*α ------- for one wheel
- α = a/r = 2/0.1 = 20 rad/s
- J = 0.5*m*r^2 = 0.5*25*0.1^2 = 0.125 kg*m^2--------------- I used 25 kg here since there are two driving wheels --> each one will accelerate half of the mass, if that makes sense. Is this assumption correct?
- T_a = J*α = 0.125*20 = 2.5 = 1/2 the T_a I previously calculated. What am I doing wrong here?
Any help is appreciated. Thanks :)
Attachments
Last edited:
 !
!