SUMMARY
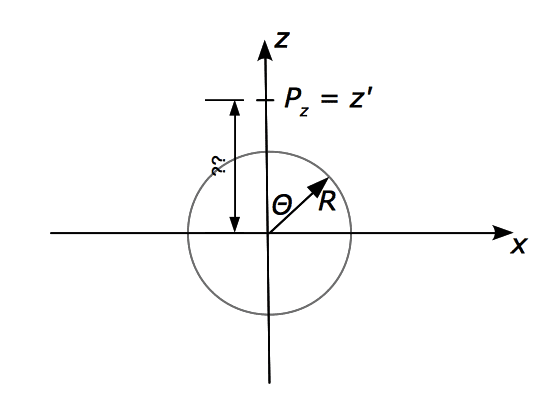
The discussion centers on calculating the dipole moment of a surface charge distribution on a spherical shell with radius R and surface charge density σ = k cos θ. The participants clarify that the z-coordinate of point P, denoted as z', can be expressed as R cos θ, which represents the z-component of the distance from the origin to a point on the surface. The dipole moment is derived using the integral p = ∫ (R cos θ)(k cos θ) R² sin θ dφ dθ, emphasizing that the dipole moment only has a z-component due to the symmetry of the charge distribution.
PREREQUISITES
- Understanding of dipole moments in electrostatics
- Familiarity with spherical coordinates and their applications
- Knowledge of surface charge density concepts
- Experience with integral calculus in physics
NEXT STEPS
- Study Griffiths' "Introduction to Electrodynamics" for a deeper understanding of dipole moments
- Learn about spherical harmonics and their role in electrostatics
- Explore the derivation of electric fields from dipole moments
- Investigate the implications of charge symmetry on electric fields and potentials
USEFUL FOR
Physics students, electrical engineers, and researchers focusing on electrostatics and electromagnetic theory will benefit from this discussion.