sweet springs
- 1,223
- 75
Best.
The discussion revolves around the effects of gravity on a thought experiment involving a train moving at relativistic speeds on a flat planet, as analyzed through the lens of special relativity and the equivalence principle. Participants explore how light behaves within the train under the influence of gravity, the implications for reference frames, and the nature of gravitational effects experienced by passengers.
Participants express multiple competing views on the behavior of light and gravity in the context of the train experiment, with no consensus reached on the correctness of the "stationary preferred" versus "passenger preferred" perspectives. The discussion remains unresolved regarding the implications of relativistic speeds on gravitational effects and reference frames.
Participants note limitations in their understanding of the equivalence principle and the complexities involved in analyzing the effects of gravity and acceleration in different frames of reference. There are unresolved mathematical steps and assumptions regarding the behavior of light and objects in the train.
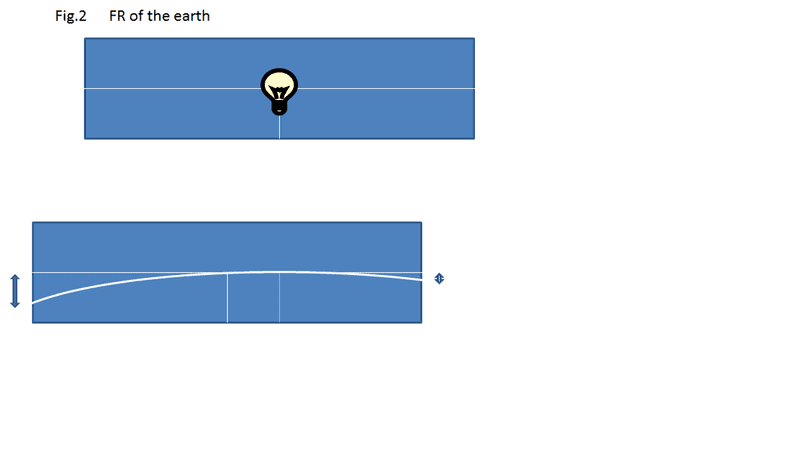
The Frame of the Earth looks correct, but It seems your train is moving to the left, which is somehow not the way I imagined it.sweet springs said:Hi. Let me draw two figures to confirm my understanding of the problem.
SlowThinker said:And the picture in train's frame is obviously not consistent with the Earth frame, or as we call it, the Rocket frame.
.
PeterDonis said:$$
\hat{e}_0 = \frac{1}{\sqrt{g^2 x^2 - v^2}} \left( g x \cosh g t \, \partial_T + g x \sinh g t \, \partial_X + v \, \partial_Y \right)
$$
$$
\hat{e}_1 = \sinh g t \, \partial_T + \cosh g t \, \partial_X
$$
$$
\hat{e}_2 = \frac{1}{\sqrt{g^2 x^2 - v^2}} \left( v \cosh g t \, \partial_T + v \sinh g t \, \partial_X + g x \, \partial_Y \right)
$$
$$
\hat{e}_3 = \partial_Z
$$
This tetrad is obviously orthonormal, and ##\hat{e}_0## is the same 4-velocity field that you and I derived; ##\hat{e}_2## is the linear combination of ##\partial_\tau## and ##\partial_\psi## that I referred to.
pervect said:Do you happen to have an expression for the basis vectors ##\hat{e}_1, \hat{e}_2, \hat{e}_3## in terms of Minkowskii coordinates ##T, X, Y, \partial_T, \partial_X, \partial_Y##
pervect said:or in terms of ##t,x,y,\partial_t, \partial_x, \partial_y##
PeterDonis said:the 4-velocity of observers at rest in his chart is the same as for ours
PeterDonis said:This is pretty straightforward too, and turns out to be, using coordinates ##t, x, y## (note that ##\eta## is the coordinate that DrGreg originally used, but we can write ##\partial_y## instead of ##\partial_\eta##, with ##y## being the Rindler ##y## coordinate, since the two partial derivatives are the same and ##y## never appears explicitly so we don't have to worry that it isn't the same as ##\eta##):
$$
\hat{e}_0 = \frac{1}{\sqrt{g^2 x^2 - v^2}} \partial_t + \frac{v}{\sqrt{g^2 x^2 - v^2}} \partial_y
$$
$$
\hat{e}_1 = \partial_x
$$
$$
\hat{e}_2 = \frac{v}{g x \sqrt{g^2 x^2 - v^2}} \partial_t + \frac{gx}{\sqrt{g^2 x^2 - v^2}} \partial_y
$$
$$
\hat{e}_3 = \partial_z
$$
Note that we use the Rindler metric to compute norms and inner products for the above, so, for example, ##\hat{e}_0 \cdot \hat{e}_2 = g^2 x^2 \left( \hat{e}_0 \right)^t \left( \hat{e}_2 \right)^t -
\left( \hat{e}_0 \right)^y \left( \hat{e}_2 \right)^y = \left( v g x - v g x \right) / \left( g^2 x^2 - v^2 \right) = 0## as desired.
pervect said:Christoffel symbols in this basis
sweet springs said:Lorentz transformation
sweet springs said:the term dxdt in ds^2 does not vanish
sweet springs said:Hi. Let me confirm my understanding the situation. In Rindler coordinates
$$ds^2 = (1+\frac{gz}{c^2})^2 c^2dt^2 - dx^2 - dy^2 - dz^2, \; \forall z>-\frac{c^2}{g}, \forall t, x, y \,.$$
Lorentz transformation,
$$
t' = \gamma \left(t - \frac{v x}{c^{2}} \right)
x' = \gamma (x - v t)\,
y' = y\,
z' = z\,$$
where
$$\gamma \equiv \frac{1}{\sqrt{1 - v^2/c^2}}$$
or
$$
t = \gamma \left(t' + \frac{v x'}{c^{2}} \right)
x = \gamma (x' + v t')\,
y = y'\,
z = z'\,$$
Putting them toghether we find the term dxdt in ds^2 does not vanish. This term causes the different manner of forward and backward lights.
DrGreg said:Oops again. Not my lucky day.
In my haste to correct my error in post #156, I overcorrected in post #159 and still got it wrong. I now think the correct answer for the quotient space metric should be <br /> \mathrm{d}s^2 =<br /> \mathrm{d}x^2<br /> + \frac{g^2x^2}{g^2x^2-v^2} \, \mathrm{d} \eta^2<br />
That can be made isometric but it's a really ugly and complicated expression, so I won't bother here.
3.2 The local spatial geometry of the rotating frame
We can introduce the local spatial geometry of the disk, which defines the
proper spatial line element, on the basis of the local optical geometry. To this
end we can use the radar method...
Let Π be a point in the rotating frame, where a light source, a light absorber
and a clock are lodged; let Π' be a near point where a reflector is lodged. The
world-lines of these points are the time like helices
...
(see figure 1). A light signal is emitted by the source in Π and propagates along the null world-
line toward Π' here it is reflected back to Π (along the null world-line where it is finally absorbed. Let
dτ be the proper time, read by a clock in Π, between the emission and absorption events: then,
according to the radar method, the proper distance between Π and Π'is defined by
##d\sigma = \frac{1}{2} c d\tau##
Now, we are going to parameterize these events, using the coordinates adapted
to the rotating frame, in order to obtain the explicit expression of the proper
spatial line element ...
The space-time intervals between the events of emissionE and reflection R, and between the events of reflectionR and absorption A, are null. Hence, by setting ds'^2 = 0 we can solve for dt , and obtain the two coordinate time ... [[for emission and absorption]]
sweet springs said:I correct z to z'.I find a poor point. The speed of train changes accorging to z due to time dilation effect of gravity.
Let v be speed of the train at floor level z'=0.
I appreciate if you point out other difficulties.
pervect said:Start with the following variant of the RIndler metric:
##ds^2 = -g^2 x^2 dt^2 + dx^2 + dy^2##
sweet springs said:Putting g=0, this formula does not go to Minkowsky. No problem?
stands. How is this idea?sweet springs said:correction:
<br /> ds^2=(1+\zeta)\, c^2dt'^2\,<br /> +(-1+\frac{v^2}{c^2}\zeta)dx'^2\,<br /> +2v\zeta\, dx'dt'\,<br /> -dy'^2-dz'^2<br />
where
$$ \zeta=\gamma^2\frac{gz'}{c^2}(2+\frac{gz'}{c^2})$$
sweet springs said:Hi. Lorentz transgfotmation is applicable to Rindler coordinates
pervect said:I'm not sure exactly what you're trying to say,
sweet springs said:I am happy to share beauty of the metric with you.
I will add some words here.
Mechanics of Billiard on the horizontal flat tables satisfies SR or Lorentz transformation even under the presence of gravity of the Earth.
Say there are stories of Billiard tables where ball movements satisfies SR on their proper layers.
Say balls on all the layers move in a perpendicular line. The perpendicular line represents wall or column of the train.
Their velocities measured at their proper tables are different due to clock pace change by height.
Though different Lorentz transformation of different speed for layers are applied, they all are expressed by one parameter v, the speed at z'=0 or any other height prefixed.
Yes, in gravitational field, or in an accelerating rocket, one speed of train is preferred among others.sweet springs said:Thus we can identify unike coordinate in Rindler system in spite of presumed equality of the coordinates.
is not true.sweet springs said:Mechanics of Billiard on the horizontal flat tables satisfies SR or Lorentz transformation even under the presence of gravity of the Earth.