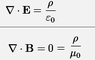SUMMARY
The discussion centers on the analogy between electric and magnetic potentials, specifically addressing the absence of magnetic monopoles and the implications for deriving magnetic potential energy formulas. The scalar potential in magnetostatics is defined as Vm=(μ0/4π)Ω⋅I, where I is the current and Ω is the solid angle. The relationship B=-∇Vm parallels the electric field's relationship with electric potential, E=-∇V. However, due to the lack of magnetic charge, a direct equivalent to electric potential energy cannot be established, although magnetic potential energy can be calculated using the vector potential.
PREREQUISITES
- Understanding of electromagnetic theory, particularly Maxwell's Equations.
- Familiarity with scalar and vector potentials in electromagnetism.
- Knowledge of magnetic fields and their properties, including magnetic dipole moments.
- Basic calculus, particularly gradient and curl operations.
NEXT STEPS
- Study the derivation of magnetic scalar potential and its applications in magnetostatics.
- Explore the concept of magnetic vector potential and its relationship to magnetic fields.
- Investigate the implications of magnetic monopoles in theoretical physics.
- Learn about energy stored in magnetic fields and the formulas used to calculate it.
USEFUL FOR
Students and professionals in physics, particularly those specializing in electromagnetism, electrical engineers, and researchers exploring theoretical physics concepts related to magnetic fields.