idmena
- 14
- 0
Hello all, I hope you can give me a hand with a QFT homework I'm working on. We are to compute the beta equation of a Non-abelian SU(N) theory with: Complex scalars (massless), bosons, ghosts. My question is referring to the Boson self-energy scalar loop correction.
1. Homework Statement
We have the boson self energy correction involving a scalar loop.
This loop is formed of 2 3-vertex of Boson-scalar-scalar:
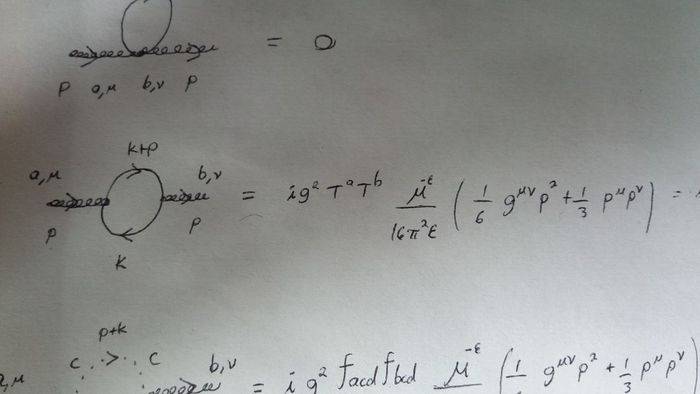
The Feynman rules I derived for this diagrams are:

Where solid lines are scalars and dashed lines are ghosts.
This is what I get:
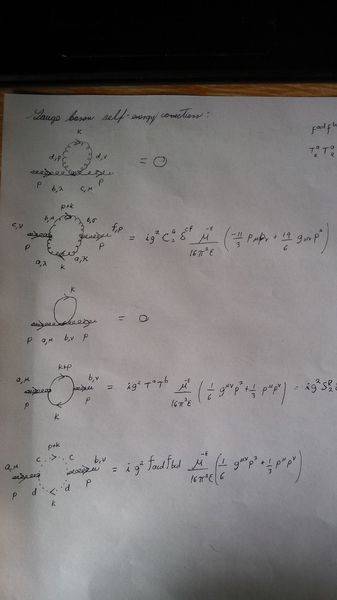
(We are setting the scalars to be massless). I know the boson loop and the ghost loop are corrrect as I checked them on a book (I'm using Bailin & Love).
The reason of my confusion is, when I add them all I get, besides some factors:
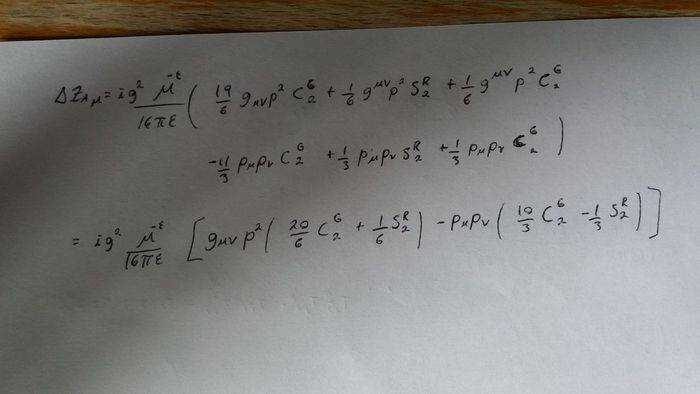
But on the lecture our teacher told us we should get:
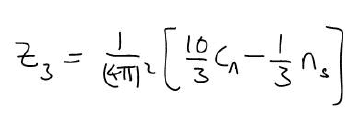
I have a sign and a factor on 2 wrong, and It's coming from the scalar loop diagram.
As we can see from the feynman rules, the 3-vertex for boson-scalar is the same as the one for boson-ghost, except for a factor. Doesn't these mean that both self-energy corrections should give me the same answer, except for such factor? And, therefore, if I know the ghost loop is correct, then I also know the scalar loop should have the same form (given the scalars are massless, as mentioned previously). But then, I am missing the (-) sign and the factor of two.
Can you help me with this please? Can someone confirm the Feynman rule I got for boson-scalar-scalar is correct? If so, where might the problem be?
Thank you very much
Regards
1. Homework Statement
We have the boson self energy correction involving a scalar loop.
This loop is formed of 2 3-vertex of Boson-scalar-scalar:
Homework Equations
The Feynman rules I derived for this diagrams are:
Where solid lines are scalars and dashed lines are ghosts.
The Attempt at a Solution
This is what I get:
(We are setting the scalars to be massless). I know the boson loop and the ghost loop are corrrect as I checked them on a book (I'm using Bailin & Love).
The reason of my confusion is, when I add them all I get, besides some factors:
But on the lecture our teacher told us we should get:
I have a sign and a factor on 2 wrong, and It's coming from the scalar loop diagram.
As we can see from the feynman rules, the 3-vertex for boson-scalar is the same as the one for boson-ghost, except for a factor. Doesn't these mean that both self-energy corrections should give me the same answer, except for such factor? And, therefore, if I know the ghost loop is correct, then I also know the scalar loop should have the same form (given the scalars are massless, as mentioned previously). But then, I am missing the (-) sign and the factor of two.
Can you help me with this please? Can someone confirm the Feynman rule I got for boson-scalar-scalar is correct? If so, where might the problem be?
Thank you very much
Regards