What is the length of x in this triangle?

  • Context: MHB 
  • Thread starter Thread starter ketanco
  • Start date Start date
  • Tags Tags
    Angle Triangle
Click For Summary

Discussion Overview

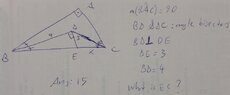
The discussion revolves around determining the length of a side, denoted as x, in a triangle based on a provided diagram. Participants explore geometric relationships and similarity of triangles, while emphasizing the constraints of solving the problem without tools during a test.

Discussion Character

  • Debate/contested
  • Mathematical reasoning
  • Conceptual clarification

Main Points Raised

  • One participant states that BE = 5 and suggests using angle bisector ratios to find x, but encounters difficulties with the equations.
  • Another participant critiques the scale of the diagram and recommends redrawing it for clarity.
  • A participant insists that the test requires solving the problem using geometric knowledge without tools, emphasizing the need for a quick solution.
  • One participant proposes extending line BD to point F and suggests expressing angles to deduce similar triangles.
  • Another participant claims to have extended line BD to F and identifies relationships between segments DF, DE, EC, and FC, but struggles with the resulting equations.
  • A later reply challenges the claim that triangles ABC and DBE are similar, indicating a potential error in reasoning.
  • A participant shares a coordinate-based representation of the triangle, aiming to clarify the relationships between the points and triangles involved.
  • Repeated emphasis on the need for a diagram that is easier to interpret, while reiterating the constraints of the test environment.

Areas of Agreement / Disagreement

Participants express differing views on the validity of the proposed geometric relationships and the necessity of a scaled diagram. There is no consensus on the correct approach to solving for x, and multiple competing interpretations of the triangle's properties remain unresolved.

Contextual Notes

Participants acknowledge the limitations of the diagram's scale and the constraints of solving the problem under test conditions without tools. There are unresolved mathematical steps and assumptions regarding triangle similarity.

ketanco
Messages
15
Reaction score
0
Hello,
what is the length of x in the attached?
I tried the following:
of course BE = 5, and also the point D must be the center of internal circle that is tangent to triangle and from there i came up with some equations together with the side ratio formulas of angle bisectors but it didnt work...

answer supposed to be 15

View attachment 8588
 

Attachments

  • 03-04.jpg
    03-04.jpg
    22.4 KB · Views: 176
Mathematics news on Phys.org
Your diagram is way out of scale.
Suggest you redraw it, making CE approx. 3 times BE.
Then extend BD to F (F on AC).
 
i know my diagram is out of scale. and that is not the question here.

we are supposed to solve this question in a test by knowledge of geometry, without using any rulers or calculators or anything, in 1-2 minutes. so we do not have the means or time to draw this to scale and solve it like that. everybody can do that. i would not take the time and effort to post it here, if i was allowed to do that. i can draw it in autocad and measure it too then... but this is not what is wanted, or something we can do during the test. we need to solve this by our knowledge of geometry, even if it is out of scale. . we will have only a pencil and a paper and an eraser when solving this.
 
1. Extend BD to F on AC as Wilmer suggested.
2. Express all angles in ${}_{{}^\times}$ and ${}_{{}^\times}\!{}_{{}^\times}$.
3. Deduce which triangles are similar.
4. Deduce the lengths of all sides, including $x$.
 
i extended the line to new point F
DF = DE = 3 as they are similar triangles with one side equal
also EC = FC now
after that ABC = DBE and i get some equations with really high numbers which also didnt give the result so either i made the equation wrong or something else... anyway, this is the way to go then...
 
ketanco said:
i extended the line to new point F
DF = DE = 3 as they are similar triangles with one side equal
also EC = FC now
after that ABC = DBE and i get some equations with really high numbers which also didnt give the result so either i made the equation wrong or something else... anyway, this is the way to go then...

Looks good!
But ABC is not similar to DBE...
 
It looks like this, doesn't it?
[TIKZ]
\coordinate[label=above:A] (A) at ({2*atan2(3,4)}:{4*7/5});
\coordinate[label=left:B] (B) at (0,0);
\coordinate[label=right:C] (C) at (20,0);
\coordinate[label=above left:D] (D) at ({atan2(3,4)}:4);
\coordinate[label=below:E] (E) at (5,0);
\coordinate[label=above right:F] (F) at ({atan2(3,4)}:7);

\draw[rotate={180+2*atan2(3,4)}] (A) +(0.4,0) -- +(0.4,0.4) -- +(0,0.4);
\draw[rotate={atan2(-3,-4)}] (D) +(0.4,0) -- +(0.4,0.4) -- +(0,0.4);
\path (B) node at +({atan2(3,4)/2}:0.7) {$\times$};
\path (B) node at +({atan2(3,4)*3/2}:0.7) {$\times$};
\path (C) node at +({180-atan2(4*7/5,15+3*7/5)/4}:3) {$\times\!\times$};
\path (C) node at +({180-atan2(4*7/5,15+3*7/5)*3/4}:3) {$\times\!\times$};

\draw (B) -- node
{4} (D) -- node
{3} (E) -- node[above] {5} cycle;
\draw (C) -- (D) -- node[below right] {3} (F);
\draw[blue, ultra thick] (A) -- (B) -- (C) -- cycle;
\path (A) -- node
{$4\cdot\frac 75$} (B) (E) -- node[below] {$x$} (C) -- node[above right] {$x$} (F);
\path (A) -- node[above] {$3\cdot\frac 75$} (F);
[/TIKZ]
Perhaps it's easier to see the similar triangles now. (Thinking)​
 
ketanco said:
i know my diagram is out of scale. and that is not the question here.

we are supposed to solve this question in a test by knowledge of geometry, without using any rulers or calculators or anything, in 1-2 minutes. so we do not have the means or time to draw this to scale and solve it like that. everybody can do that. i would not take the time and effort to post it here, if i was allowed to do that. i can draw it in autocad and measure it too then... but this is not what is wanted, or something we can do during the test. we need to solve this by our knowledge of geometry, even if it is out of scale. . we will have only a pencil and a paper and an eraser when solving this.
That's all ok, buddy, but beside the point:
what I meant was making a diagram that's easier "to follow".
We're not taking "the test"...
 

Similar threads

MHB Difference of angles in a triangle
  • · Replies 4 ·
Replies
4
Views
2K
MHB Find Length of Side in Right Triangle w/ 45°, 90°, and 45° Angle
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Geometry problem of interest with a 3-4-5 triangle
  • · Replies 59 ·
2
Replies
59
Views
154K
MHB Finding the Leg Lengths of a Right Triangle with an Acute Angle of 22°
  • · Replies 2 ·
Replies
2
Views
1K
MHB [ASK] Find the ratio of the area of triangle BCH and triangle EHD
  • · Replies 4 ·
Replies
4
Views
2K
MHB Can You Find the Angle in This Isosceles Triangle Problem?
  • · Replies 1 ·
Replies
1
Views
1K
MHB Proving Equality of Angles in an Acute Triangle
  • · Replies 4 ·
Replies
4
Views
1K
MHB Acute angle of right triangles
  • · Replies 4 ·
Replies
4
Views
2K
MHB What is the minimum value for x in this triangle with angle bisectors AD and BD?
  • · Replies 1 ·
Replies
1
Views
1K
MHB Length of sides of right triangle with 1 angle and 1 side
  • · Replies 2 ·
Replies
2
Views
2K