CAF123
Gold Member
- 2,918
- 87
Homework Statement
Helmholtz coils can be modeled as a pair of current loops oriented so that they are parallel to each other with a common axis in the x direction. The two loops have the same current I, and the same radius R, and their centres are at x = -d and x = +d, so the distance between the two loops is 2d.
(a) Write down the magnetic field at position x along the axis of the coils. What is the magnetic field at the midpoint between the coils, i.e. at x = 0? What is the magnetic field at x >> R
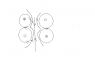
Sketch the magnetic field lines for all r.
Homework Equations
B field from a single coil
The Attempt at a Solution
Put the x-axis horizontally with +ve x pointing rightwards. Then as you look in positive x, the loops have clockwise currents. The B field along the x-axis for a single coil is $$\vec{B} = \frac{\mu_o I R^2}{2(R^2+x_1^2)^{3/2}}\underline{e}_x,$$ where ##x_1## is the B field at a distance x1 from coil 1.
With the coils having the same orientation of current, both B fields will be in +ve x, so the total B field is given by: $$\frac{\mu_o I R^2}{2} \left(\frac{1}{(R^2+x_1^2)^{3/2}} + \frac{1}{(R^2 + x_2^2)^{3/2}}\right)$$ I can write ##x_1 = x - d## and ##x_2 = x + d##. Sub these in gives the first part. Sub x=0 for the second part: $$\vec{B}_{0} = \frac{\mu_o I R^2}{(R^2+d^2)^{3/2}}\underline{e}_x$$ For x >>R, taylor expand to give $$\vec{B}_{x>>R} = \frac{\mu_o I R^2}{2} \left(\frac{1}{(x-d)^3} + \frac{1}{(x+d)^3}\right)$$
Is that ok? For the B field lines for all r, I have attached a sketch of what I have. I think the B field should be circular around the coil and obviously straight along the x axis. I am not too sure about the region between the two coils.
Many thanks.