noamriemer
- 50
- 0
Hi!
There is a concept I don't understand and would love to have is cleared...
What is the meaning of a lattice with a basis?
What do I need it for?
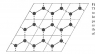
Say I have a honeycomb structure. (fig 1) and a basis as mentioned there (did I understand it right? is it the basis? )
why does it become a simple lattice spanned by ax,ay,az
with a two point basis
0, a/2(x+y+z)
or a four -point basis
0, a/2(x+y), a/2(x+z), a/2(y+z) ?
I don't understand the whole thing. For a start, how can in be (mathematically) that 0 is a part of a basis? What is this 0?
Second thing, how can something be spread by either 2 or 4 dimension basis?
It does not fit what I know about a basis...
I can't find answers to these questions... and I guess I miss the whole concept...
Thank you in advance for your help :)
There is a concept I don't understand and would love to have is cleared...
What is the meaning of a lattice with a basis?
What do I need it for?
Say I have a honeycomb structure. (fig 1) and a basis as mentioned there (did I understand it right? is it the basis? )
why does it become a simple lattice spanned by ax,ay,az
with a two point basis
0, a/2(x+y+z)
or a four -point basis
0, a/2(x+y), a/2(x+z), a/2(y+z) ?
I don't understand the whole thing. For a start, how can in be (mathematically) that 0 is a part of a basis? What is this 0?
Second thing, how can something be spread by either 2 or 4 dimension basis?
It does not fit what I know about a basis...
I can't find answers to these questions... and I guess I miss the whole concept...
Thank you in advance for your help :)