What is the minimum time at a given angle on a cone with constant size?

[bowes78]

Homework Statement

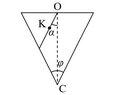
A hollow cone is placed on the ground like shown in example. Inside a cone there is string attached to base center. In the string there is a small bead. What must the angle between string and vertical be, so bead reaches cone surface fastest? (You can stretch the string). Cone base is parallel to the ground and cone has angle φ. String frictionless.

Relevant Equations

kinematic eqs
trig identites

I tried to come up with expression of time in terms of φ, α, and some constant value of cone size that does not depend on angle (I used R as cone radius). I though I could use that expression to see at what angle time is going to minimum, but I came up with expression from which I can't make a conclusion. I believe there is another solution method, or maybe there are some useful trig identities, but I was unable to find it.
Can someone help me out? Thanks

Angle φ is marked badly at my solution, but that doesn't change anything in particular.

 

[kuruman]

Note that the angle you call $\varphi$ is half the angle given as $\varphi$ in the diagram.

My first approach would be to use the law of sines for the triangle that has angles $\alpha$, $\varphi/2$ and $\pi-(\alpha+\varphi/2).$ Then minimize $t^2$ with respect to $\alpha.$

 

[bowes78]

Note that the angle you call $\varphi$ is half the angle given as $\varphi$ in the diagram.

My first approach would be to use the law of sines for the triangle that has angles $\alpha$, $\varphi/2$ and $\pi-(\alpha+\varphi/2).$ Then minimize $t^2$ with respect to $\alpha.$

So I get t^2=(2 a sin(φ/2))/(g cosα sin(φ/2+α)), a is length OC. How can I minimize it to find value of α?

 

[haruspex]

So I get t^2=(2 a sin(φ/2))/(g cosα sin(φ/2+α)), a is length OC. How can I minimize it to find value of α?

How do you usually find a minimum of a function wrt its independent variable?

 

[bowes78]

How do you usually find a minimum of a function wrt its independent variable?

So after differentiation with respect to α, setting t=0, I get α=90-(φ/2). Could this be the answer?

 

[haruspex]

So after differentiation with respect to α, setting t=0, I get α=90-(φ/2). Could this be the answer?

Consider what that looks like in your diagram. It would mean the string meets the cone at a right angle. It is easy to show that the answer must have the string meet the cone somewhat lower.
If you cannot find your error, please post your working.

 

[bowes78]

Consider what that looks like in your diagram. It would mean the string meets the cone at a right angle. It is easy to show that the answer must have the string meet the cone somewhat lower.
If you cannot find your error, please post your working.

Yes, previous solution had a mistake. This time I tried to do something like this, but that seems to me that it doesn't make sense too. Because if we set (φ/2)=0, then α=32, which doesn't look right.

 

[kuruman]

What about the work before what you posted? Specifically, what does $a$ stand for in the first equation giving $t^2$?

 

[bowes78]

What about the work before what you posted? Specifically, what does $a$ stand for in the first equation giving $t^2$?

I just picked there wrong trigonometry formulas, so I got wrong answer. As I mentioned before, a is length OC in the triangle. I needed that for law of sines.

 

[kuruman]

The law of sines is always two equations. In this case is $$\frac{s}{\sin\alpha}
=\frac{\frac{1}{2}gt^2\cos\alpha}{\sin(\varphi/2)}
=\frac{h}{\sin(\alpha+\varphi/2)}.
$$
Did you use both? The first equation involving segment $s$ is needed to ensure that the point of intersection P is on the hypotenuse at time $t$.

It's probably easier and more straightforward to write equations for the position of the bead, $x(t)$ and $y(t),$ find the intersection with the hypotenuse and then minimize.

 

[haruspex]

Yes, previous solution had a mistake. This time I tried to do something like this, but that seems to me that it doesn't make sense too. Because if we set (φ/2)=0, then α=32, which doesn't look right.

Not sure how you got the line following "=>". Please post the details of that step.
I assume you realise it is only necessary to maximise the denominator in the expression for $t^2$ since the numerator is constant.

 

[bowes78]

The law of sines is always two equations. In this case is $$\frac{s}{\sin\alpha}
=\frac{\frac{1}{2}gt^2\cos\alpha}{\sin(\varphi/2)}
=\frac{h}{\sin(\alpha+\varphi/2)}.
$$
Did you use both? The first equation involving segment $s$ is needed to ensure that the point of intersection P is on the hypotenuse at time $t$.

It's probably easier and more straightforward to write equations for the position of the bead, $x(t)$ and $x(t)$ find the intersection with the hypotenuse and then minimize.
View attachment 318945

No, I used only $$\frac{h}{sin(\alpha+\varphi/2)}=\frac{\frac{1}{2}gt^{2}cos\alpha }{sin(\varphi/2) }.$$

I think I'm getting your idea, but how I should write $x(t)$ equation? I suppose that $$y(t)=\frac{1}{2}gt^{2}.$$
Or it should be like $$y(t)=\frac{1}{2}gcos^{2}\alpha t^{2} $$
$$x(t)=\frac{1}{2}gsin\alpha cos\alpha t^{2}$$
Because string length is $${\frac{1}{2}gcos\alpha}t^{2}$$

 

[bowes78]

Not sure how you got the line following "=>". Please post the details of that step.
I assume you realise it is only necessary to maximise the denominator in the expression for $t^2$ since the numerator is constant.

 

[haruspex]

View attachment 318986

a and φ are constants, so what is the derivative of $2a\sin(\phi/2)$?

 

[bowes78]

a and φ are constants, so what is the derivative of $2a\sin(\phi/2)$?

I see... It should be zero, but whole equation then disappears.

 

[haruspex]

I see... It should be zero, but whole equation then disappears.

Does it? What do you have left?

 

[bowes78]

Does it? What do you have left?

Well, should I solve it like that?
$$-gcos(2\alpha+\varphi /2)(2asin(\varphi/2))=0$$
$$cos(2\alpha+\varphi /2)=0$$
$$\alpha =\frac{90^{\circ}-\varphi /2 }{2}$$

 

[haruspex]

Well, should I solve it like that?
$$-gcos(2\alpha+\varphi /2)(2asin(\varphi/2))=0$$
$$cos(2\alpha+\varphi /2)=0$$
$$\alpha =\frac{90^{\circ}-\varphi /2 }{2}$$

Right.

 

[bowes78]

Right.

Thanks!