What is the minimum value for x in this triangle with angle bisectors AD and BD?

[ketanco]

Hello,

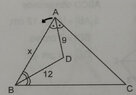
In the attached, what is the minimum integer value x can take?

AD and BD are angle bisectors

the answer is 16 - but i do not know how they did it

I am totally stuck, could not think of anything here. The angle bisector formula I know does not fit hereView attachment 8569

 

[Opalg]

View attachment 8570

Here is an intuitive idea of what this question is about. It's up to you to express it mathematically!

Suppose we keep $B$ and $D$ fixed, and imagine what happens as we try to reduce $x$ by rotating the line $AD$ around $D$, as indicated in the diagram. As the angles at $A$ and $B$ increase, $C$ will be pushed further and further away from $D$.

If the obtuse angle $ADB$ is reduced to a right angle, then (by Pythagoras) $x$ will have been reduced to $15$. But in that case, the angles $DAB$ and $DBA$ will add up to $90^\circ$. So the angles $CAB$ and $CBA$ will add up to $180^\circ$. In other words, $AC$ will be parallel to $BC$ (or to put it another way $C$ will have gone off to infinity). In that case, $ABC$ will no longer be a triangle.

The conclusion from that is that $x$ cannot be reduced to $15$. So the smallest integer value that it can take must be $16$.