OhNoYaDidn't
- 25
- 0
This problem was on my exam last week, and I've been having some troubles coming up with a solution.
1. Homework Statement
Two semi-infinite conducting planes are connected by insulating glue, they make a 30º angle with each other. One of them is at ground potential, and the other one at V0. Find the potential between the conductors.
Note: There might be solutions, in which the potential has logarithmic dependence on the distance to the axis, or even independent of this distance.
Laplace's equation in cylindrical coordinates.
3. The Attempt at a Solution [/B]
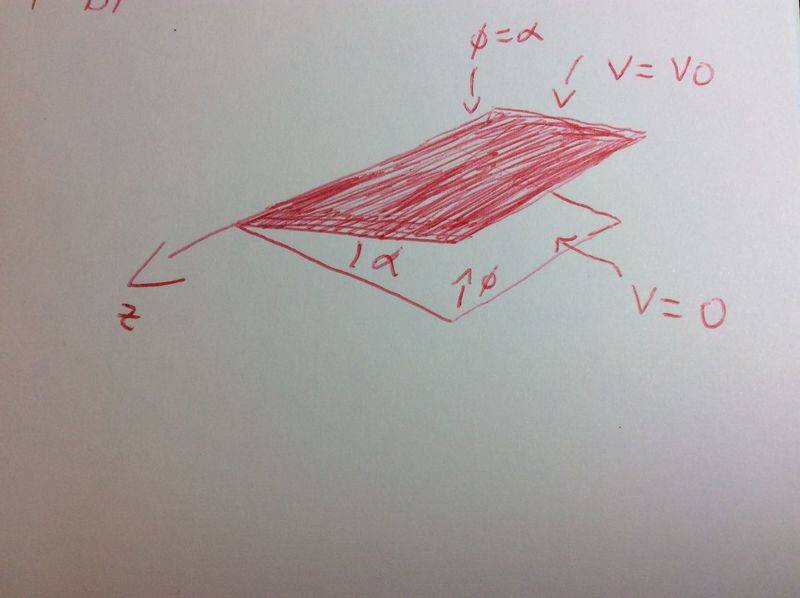
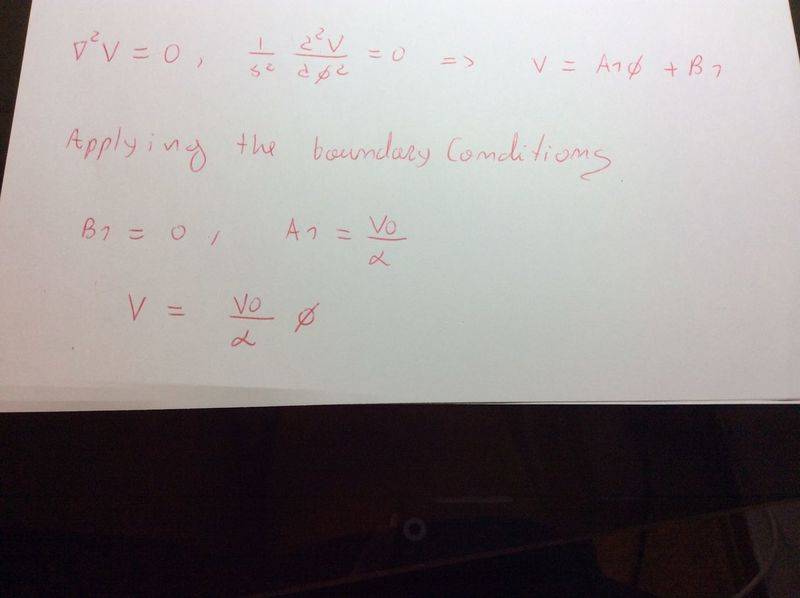
The boundary conditions i came up with are:
1- V=0 at phi=0
2- V=V0 at phi=alpha
But I'm note sure if this is right.
Can you guys please help me out?
1. Homework Statement
Two semi-infinite conducting planes are connected by insulating glue, they make a 30º angle with each other. One of them is at ground potential, and the other one at V0. Find the potential between the conductors.
Note: There might be solutions, in which the potential has logarithmic dependence on the distance to the axis, or even independent of this distance.
Homework Equations
Laplace's equation in cylindrical coordinates.
3. The Attempt at a Solution [/B]
The boundary conditions i came up with are:
1- V=0 at phi=0
2- V=V0 at phi=alpha
But I'm note sure if this is right.
Can you guys please help me out?