SUMMARY
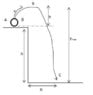
The proper formula for the maximum height, denoted as ##Y_{max}##, for a projectile trajectory is given by ##y_{max} = \frac{V^{2}sin^{2}θ}{2g} + H##, where ##H## represents the height of the launch point. The horizontal range formula is correctly identified as ##R = \frac{V^{2}sin 2θ}{g}##, which is distinct from the maximum height calculation. The discussion clarifies common misconceptions regarding the relationship between horizontal range and maximum height in projectile motion.
PREREQUISITES
- Understanding of basic projectile motion concepts
- Familiarity with trigonometric identities, particularly ##\sin 2θ##
- Knowledge of kinematic equations in physics
- Ability to manipulate algebraic expressions involving variables
NEXT STEPS
- Study the derivation of projectile motion equations in physics
- Learn about the effects of initial height on projectile trajectories
- Explore the application of trigonometric identities in physics problems
- Investigate the impact of air resistance on projectile motion
USEFUL FOR
Students of physics, educators teaching projectile motion, and anyone involved in engineering or design requiring an understanding of trajectory calculations.