Particle projected from above a dome

[Bling Fizikst]

Homework Statement

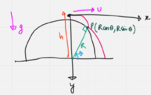
refer to image

Relevant Equations

refer to image

Since the ball will follow a parabolic trajectory , i threw it into the coordinate plane with particle starting from the origin .

$$y= kx^2$$ Differentiating wrt $t$ : $$ gt=2ku^2 t\implies u=\sqrt{\frac{g}{2k}}$$ where $$k=\frac{\sin\theta}{R\cos^2\theta}$$ Now , final speed when it reached the bottom is $$\sqrt{u^2+2gh}$$ but I am stuck here on how to find $h$ in terms of $\theta$ in order to minimise the expression .

 

[PeroK]

Are you sure you don't have to further analyse the collision with the sphere?

 

[PeroK]

Now , final speed when it reached the bottom is $$\sqrt{u^2+2gh}$$ but I am stuck here on how to find $h$ in terms of $\theta$ in order to minimise the expression .

What you've shown is that the final speed is independent of the angle. That's a consequence of conservation of energy.

 

[Bling Fizikst]

Are you sure you don't have to further analyse the collision with the sphere?

Maybe i misinterpreted the 'touching' of the dome . So , the correct interpretation should be that the ball collides with the dome and changes its trajectory and then strikes the ground ? I attached the figure . @Hill , yeah absolutely ! i was careless . It should be $P(R\cos\theta ,h-R\sin\theta)$

 

[Hill]

By the sketch, it appears that coordinates of the point P are $(R \cos \theta, R \sin \theta)$. This is incorrect if the particle starts from the origin.

 

[PeroK]

Maybe i misinterpreted the 'touching' of the dome . So , the correct interpretation should be that the ball collides with the dome and changes its trajectory and then strikes the ground ?

We can minimise the energy to $mgh$ by setting $u \approx 0$. Why isn't that allowed? The reason must be that the ball will impact the dome more than once. Perhaps the constraint is that the ball must hit the dome once and only once?

That was my thinking

 

[Hill]

Because of the post #5 above, the $$k=\frac{\sin\theta}{R\cos^2\theta}$$is incorrect.

 

[Hill]

@Hill , yeah absolutely ! i was careless . It should be $P(R\cos\theta ,h-R\sin\theta)$.

Yes, but in fact you don't need $\theta$ at all.

 

[PeroK]

We can minimise the energy to $mgh$ by setting $u \approx 0$. Why isn't that allowed? The reason must be that the ball will impact the dome more than once. Perhaps the constraint is that the ball must hit the dome once and only once?

That was my thinking

I don't think this can be right. The problem gets too complicated. Instead, I think the question might assume that the ball is moving tangential to the sphere at the point of impact. That assumption leads to a solvable problem.

@Hill is that what you assumed?

 

[Hill]

I think the question might assume that the ball is moving tangential to the sphere at the point of impact. That assumption leads to a solvable problem.

@Hill is that what you assumed?

Yes, that is what I thought.

 

[Bling Fizikst]

Was my original diagram correct then? If yes , after correction (thanks to @Hill) . I am getting $$\mid v_{\min}\mid =\sqrt{2gR(\sin\theta\pm \cos\theta)}$$ for $\theta\in\left(0,\frac{\pi}{2}\right)$ . Not sure how to proceed from here . The calculation looks tricky as i have to make cases for everything now. For instance , i took $\sin\theta +\cos\theta \geq 1$ and again you get different answers for taking $\theta=0^{+}$ or ${\frac{\pi}{2}}^{-}$ . All of them being wrong btw.

 

[PeroK]

Was my original diagram correct then? If yes , after correction (thanks to @Hill) . I am getting $$\mid v_{\min}\mid =\sqrt{2gR(\sin\theta\pm \cos\theta)}$$ for $\theta\in\left(0,\frac{\pi}{2}\right)$ . Not sure how to proceed from here . The calculation looks tricky as i have to make cases for everything now. For instance , i took $\sin\theta +\cos\theta \geq 1$ and again you get different answers for taking $\theta=0^{+}$ or ${\frac{\pi}{2}}^{-}$ . All of them being wrong btw.

There is no need to involve theta. Note that both $u$ and $h$ are variables. You need a constraint on these to ensure that the ball impacts the sphere at a tangent.

 

[Bling Fizikst]

There is no need to involve theta. Note that both $u$ and $h$ are variables. You need a constraint on these to ensure that the ball impacts the sphere at a tangent.

I dont know how to go about it .

 

[PeroK]

I dont know how to go about it .

You have two curves. You need to calculate the condition so that the curves are tangent at their point of intersection.

Note that, in case you haven't already seen this, the parabolic path for an initially horizontal trajectory is:
$$y = h - \frac 1 2 gt^2, \ x = ut$$$$\implies y = h - \frac{gx^2}{2u^2}$$

 

[Hill]

How about this?
Right the equation for the point $P(x, kx^2)$ to be at the distance $R$ from the dome center $(0, h)$. You'll get a quadratic equation with solutions depending on $k$ and $h$. Right a condition when this equation has exactly one solution, i.e., the parabola has one and only one point at the distance $R$ from the dome center. This will give you dependence of $h$ on $k$. Then find $k$ that minimizes $u$.

EDIT. Sorry, minimizes not $u$ but the speed at the ground.

 

[Bling Fizikst]

How about this?
Right the equation for the point $P(x, kx^2)$ to be at the distance $R$ from the dome center $(0, h)$. You'll get a quadratic equation with solutions depending on $k$ and $h$. Right a condition when this equation has exactly one solution, i.e., the parabola has one and only one point at the distance $R$ from the dome center. This will give you dependence of $h$ on $k$. Then find $k$ that minimizes $u$.

The calculation is brutal imo , i dont think it can be calculated by hand . We might have to look for other ways to get around this?

 

[Hill]

The calculation is brutal imo , i dont think it can be calculated by hand . We might have to look for other ways to get around this?

Hmmm... You might be right. I got, by hand, to $h=\frac {1-4k^2R^2}{4k}$. (If my algebra is right.)

 

[PeroK]

The calculation is brutal imo , i dont think it can be calculated by hand . We might have to look for other ways to get around this?

It's about a page of A4 without any shortcuts. You have to knuckle down and accept that these problems are not going to be cracked in a few lines.

 

[PeroK]

Hmmm... You might be right. I got, by hand, to $h=\frac {1-4k^2R^2}{4k}$. (If my algebra is right.)

If $k = \frac {g}{2u^2}$, then I have a plus in that equation.

 

[gmax137]

You need a constraint on these to ensure that the ball impacts the sphere at a tangent.

Do we know for sure that this is the intent of the problem? I don't think it is worded very clearly.

 

[PeroK]

Do we know for sure that this is the intent of the problem?

We are pretty sure.

I don't think it is worded very clearly.

I agree. It should have been given as two steps: first find the relationship between $h$ and $u$ so that the ball touches the sphere at a tangent. Find $h$ and $u$ that minimises the speed of impact with the ground (which is equivalent to minimising the total energy of the ball (PE + KE)).

 

[Bling Fizikst]

Easily one of the worst problems for physics . Continuing from : $$(kx^2-h)^2+x^2=R^2$$ When two curves are tangent to each other at a point then there is a double root , here : $(\alpha>0)$ in it . Let $\alpha,\alpha,\beta,\gamma$ be the roots of the eqn : $$k^2x^4+(1-2hk)x^2+h^2-R^2=0$$ Define $\sigma_r$ as sum of roots taken $r$ at a time . $$\sigma_1=2\alpha+\beta+\gamma=0$$$$\sigma_4=\alpha^2 \beta\gamma=\frac{h^2-R^2}{k^2}$$ $$\sigma_3=\alpha^2(\beta+\gamma)+\beta\gamma(2\alpha)=0$$ Easily eliminating $\beta,\gamma$ in $\sigma_3$ to get : $$k^2\alpha^4=2(h^2-R^2)$$ Plugging the values of $\alpha^4,\alpha^2$ in the original equation to get :$$2k\sqrt{h^2-R^2}=2hk-1\implies h=\frac{4k^2 R^2+1}{4k}$$ Now consider the speed $$s=\sqrt{u^2+2gh}=\sqrt{2u^2+\frac{g^2 R^2}{u^2}}\geq \boxed{\sqrt{2Rg\sqrt{2}}}$$ equality at $\boxed{u=\sqrt{\frac{gR}{\sqrt{2}}}}$ $$\implies k=\frac{1}{R\sqrt{2}}\implies \boxed{h=\frac{3\sqrt{2}R}{4}}$$

 

[Hill]

Easily one of the worst problems for physics . Continuing from : $$(kx^2-h)^2+x^2=R^2$$ When two curves are tangent to each other at a point then there is a double root , here : $(\alpha>0)$ in it . Let $\alpha,\alpha,\beta,\gamma$ be the roots of the eqn : $$k^2x^4+(1-2hk)x^2+h^2-R^2=0$$ Define $\sigma_r$ as sum of roots taken $r$ at a time . $$\sigma_1=2\alpha+\beta+\gamma=0$$$$\sigma_4=\alpha^2 \beta\gamma=\frac{h^2-R^2}{k^2}$$ $$\sigma_3=\alpha^2(\beta+\gamma)+\beta\gamma(2\alpha)=0$$ Easily eliminating $\beta,\gamma$ in $\sigma_3$ to get : $$k^2\alpha^4=2(h^2-R^2)$$ Plugging the values of $\alpha^4,\alpha^2$ in the original equation to get :$$2k\sqrt{h^2-R^2}=2hk-1\implies h=\frac{4k^2 R^2+1}{4k}$$ Now consider the speed $$s=\sqrt{u^2+2gh}=\sqrt{2u^2+\frac{g^2 R^2}{u^2}}\geq \boxed{Rg\sqrt{2}}$$ equality at $\boxed{u=\sqrt{\frac{gR}{\sqrt{2}}}}$ $$\implies k=\frac{1}{R\sqrt{2}}\implies \boxed{h=\frac{3\sqrt{2}R}{4}}$$

$R$ and $g$ have numerical values in the problem.

 

[PeroK]

I had another idea to use vectors. I took the origin at the centre of the sphere. The particle's position and velocity are given by:
$$\vec x = (x, h - \frac{gx^2}{2u^2}), \ \vec v = (u, - \frac{gx} u)$$If the particle impacts the sphere at a tangent, then:
$$\vec x = (R\cos \theta, R \sin\theta) \ \text{and} \ \vec x \cdot \vec v = 0$$$$\vec x \cdot \vec v = uR\cos \theta - \frac{R^2g}{u}\sin \theta\cos \theta = 0$$$$\implies R\sin \theta = \frac{u^2}{g}$$$$\implies y = \frac{u^2}{g}, x^2 = R^2 - \frac{u^4}{g^2}$$This allows us to calculate $h$:
$$h - \frac{gx^2}{2u^2} = R \sin\theta = \frac{u^2}{g}$$$$\implies h = \frac{u^2}{2g} + \frac{R^2g}{2u^2}$$
PS note that when the energy is minimised, with $u^2 = \frac{gR}{\sqrt 2}$, then:
$$\sin \theta = \frac{u^2}{Rg} = \frac 1 {\sqrt 2}$$And $\theta = \dfrac \pi 4$.

 

[Steve4Physics]

Since the OP has posted a solution, here is a YouTube video with a different approach, if of interest.

 

[TSny]

Since the OP has posted a solution, here is a YouTube video with a different approach, if of interest.

Yes, that was slick.

At time 2:40 he uses "AM greater than or equal to GM", which didn't ring a bell. After some thought it occurred to me that AM refers to arithmetic mean and GM to geometric mean. See AM-GM inequality. That was a clever way to find the minimum of $2\cos \theta + \dfrac 1 {\cos \theta}$

 

[PeroK]

Yes, that was slick.

I think the simplest solution is to look at the distance squared, $D$, of the particle from the centre of the sphere as a function of $y$:
$$y = h - \frac{gx^2}{2u^2} \ \implies x^2 = (h-y)\frac{2u^2}{g}$$
$$D(y) = x^2 + y^2 = (h-y)\frac{2u^2}{g} + y^2$$$$D'(y) = 2y - \frac{2u^2}{g}$$Then:
$$D'(y) = 0 \implies y = \frac{u^2}{g}$$And:
$$D_{min} = \frac{2u^2}{g}h - \frac{u^4}{g^2}$$Finally:
$$D_{min} = R^2 \implies h = \frac{R^2g}{2u^2} + \frac{u^2}{2g}$$The final speed satisfies:
$$v^2 = u^2 + 2gh = 2u^2 + \frac{g^2R^2}{u^2}$$To minimise this is equivalent to minimising the function:
$$f(z) = az +\frac b z$$$$f'(z) = 0 \implies a - \frac b {z^2} = 0 \implies z^2 = \frac b a$$This gives a minimum when:
$$u^4 = \frac{g^2R^2}{2}$$$$u^2 = \frac{gR}{\sqrt 2}$$And:
$$v^2_{min} = 2\sqrt 2 gR$$

 

[TSny]

I think the simplest solution is to look at the distance squared, $D$, of the particle from the centre of the sphere as a function of $y$:

Yes, that's a very nice approach!

When you got to the following part, I couldn't resist finding the minimum of $f(z)$ using the "AM-GM Inequality":

To minimise this is equivalent to minimising the function:
$$f(z) = az +\frac b z$$

AM $= \frac 1 2 (az + \dfrac b z) = \frac 1 2 f(z)$ and GM $= \sqrt{ab}$. So, $f_{min} = 2 \sqrt{ab} = 2 \sqrt 2 gR$.

 

[PeroK]

AM $= \frac 1 2 (az + \dfrac b z) = \frac 1 2 f(z)$ and GM $= \sqrt{ab}$. So, $f_{min} = 2 \sqrt{ab} = 2 \sqrt 2 gR$.

How do you justify that in this case AM = GM? In general, AM > GM is possible.

PS We have equality if $az= \frac b z$. Interesting.

 

[PeroK]

I think you have to be careful with that technique. In general, the minimum of the function $f(z) = g(z) + h(z)$ occurs when $g'(z) + h'(z) = 0$ and not when $g(z) = h(z)$. The GM of $\sqrt{g(z)h(z)}$ may be unrelated to the minimum value.