What is the R^3 in Kepler's 3rd Law?

[phantomvommand]

Homework Statement

this isn't really homework, but I've noticed some apparent inconsistencies between the different versions of Kepler's 3rd law for various orbits

Relevant Equations

Conservation of Energy
Conservation of Angular Momentum
Period = Area / dA/dt

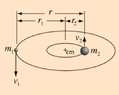
In a binary elliptical/circular orbit, the R^3 refers to the distance between the 2 planets. In the picture below, $T^2 = kr^3$.
However, for an elliptical orbit about the sun (which is assumed to be fixed as it is so heavy), and where the sun is located at a focus of the ellipse, $T^2 = ka^3$, a is the semi-major axis.
The idea that R^3 refers to the distance between the 2 planets does not agree with the 'elliptical orbit about sun' case. Is there any resolution to this?

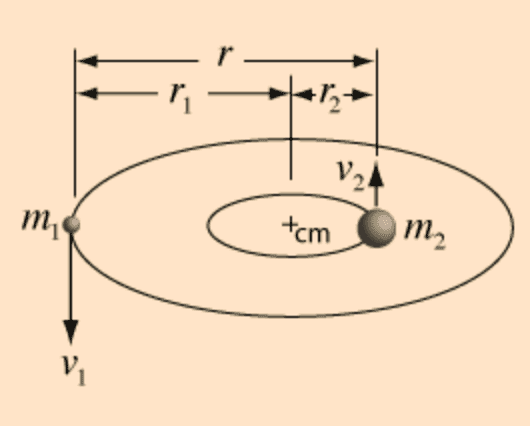
Also, for a much more general case, such as when 2 plants are both in elliptical orbit about a common centre of mass that is not at the centre of either ellipse, what is the R in the R^3? I have tried working it out, but the algebra is very difficult to resolve, if even resolvable.
My method is as such:
X1------------Y1--C---X2----------------------Y2
X1X2 and Y1Y2 represent the perigee/apogee of 2 elliptical orbits. X1X2 is 1 ellipse, and Y1Y2 another. C is the common centre of mass. One can assign a velocity for each of the 4 points X1, X2, Y1 and Y2, and assign a length for X1Y1, Y1C, CX2, X2Y2, and write down a conservation of energy equation for when planet 1 is at X1 (and plant 2 is at Y2), and when planet 1 is at X2 (and planet 2 is at Y1).
Once can also equate the periods of planet 1 and planet 2. Their periods can be found using total area of ellipse / dA/dt, and dA/dt = L/2m, although L is different for both of the planets. L is also equivalent for planet 1 at X1 and X2 (same for planet 2). Somehow, R can be found, but the algebra is too complex for me.

All help is appreciated.

 

[haruspex]

The idea that R^3 refers to the distance between the 2 planets does not agree with the 'elliptical orbit about sun' case.

I'm not seeing the contradiction. Taking the limit of one planet being infinitely massive and the orbit being circular, they converge to the same.

 

[fresh_42]

I think it is quite well explained on Wikipedia:
https://en.wikipedia.org/wiki/Kepler's_laws_of_planetary_motion#Third_law

The equation explains why the radius is cubed, and the time squared.

 

[Delta2]

I think it is quite well explained on Wikipedia:
https://en.wikipedia.org/wiki/Kepler's_laws_of_planetary_motion#Third_law

The equation explains why the radius is cubed, and the time squared.

The wikipedia article proves Kepler's laws in the case of a primary and immovable body (the Sun in the case of our solar system) that is surrounded by secondary objects in elliptical orbits. The OP is interested about Kepler's laws when the primary is moving and has its own elliptical orbit.

 

[phantomvommand]

I'm not seeing the contradiction. Taking the limit of one planet being infinitely massive and the orbit being circular, they converge to the same.

Why would the limit of the elliptical orbit become circular? In the case of a small planet's orbit about the sun, the sun can already be considered as 'infinitely massive', and the planet's orbit is still elliptical. Yet, the R refers not to the distance between the Sun and the planet at apogee, but instead refers to the semi-major axis. This disagrees with the 3 cases I mentioned above (single mass circular orbit, 2 masses circular orbit and 2 masses elliptical orbit about COM that is at centre of both ellipses).

 

[haruspex]

Why would the limit of the elliptical orbit become circular? In the case of a small planet's orbit about the sun, the sun can already be considered as 'infinitely massive', and the planet's orbit is still elliptical. Yet, the R refers not to the distance between the Sun and the planet at apogee, but instead refers to the semi-major axis. This disagrees with the 3 cases I mentioned above (single mass circular orbit, 2 masses circular orbit and 2 masses elliptical orbit about COM that is at centre of both ellipses).

The diagram in post #1 is presumably for a binary system of circular orbits, but viewed at an angle. For elliptical orbits, the COM should be at a focus for each ellipse, the other foci being separate.
For the binary elliptical case, according to @fresh_42's link, r becomes:
"the semi-major axis, a, of the elliptical relative motion of one mass relative to the other".
Note the "relative to". Does that help?

 

[phantomvommand]

The diagram in post #1 is presumably for a binary system of circular orbits, but viewed at an angle. For elliptical orbits, the COM should be at a focus for each ellipse, the other foci being separate.
For the binary elliptical case, according to @fresh_42's link, r becomes:
"the semi-major axis, a, of the elliptical relative motion of one mass relative to the other".
Note the "relative to". Does that help?

Thanks so much for the COM and relative motion clarification. I think the relative motion note could also answer the more general double elliptical orbit case mentioned at the bottom of post #1. Let me restate the diagram and symbols:

X1------Y1--C---X2----------Y2, where X1X2 represent the perigee/apogee of 1 elliptical orbit, similarly for Y1Y2. C is the centre of mass located at the common foci of both ellipses.
Let $X1C = a_1, CY2 = a_2, Y1C = a_3, CX2 = a_4$
The "R" for such a system would be $\frac {a_1 + a_2 + a_3 + a_4} {2}$.
Am I right?

 

[TSny]

For the general case where $m_1$ and $m_2$ orbit in ellipses about their center of mass, the period $T$ of the orbits satisfies the relation $$T^2 = \left(\frac{4 \pi^2}{G M} \right ) a^3$$ where $M = m_1 + m_2$ and $a = a_1 + a_2$. Here, $a_1$ and $a_2$ are the semimajor axes of the ellipses traced by $m_1$ and $m_2\,$, respectively.

Since a circle may be thought of as an ellipse of zero eccentricity, this formula applies also to the case where the two masses are in circular orbits about their center of mass. $a_1$ and $a_2$ are then just the radii of the circular orbits.

As an example, you can have two particles of equal mass $m$ orbiting each other in a circular orbit of radius $R$

The period of each mass is then determined by $$T^2 = \left(\frac{4 \pi^2}{G M} \right ) a^3 = \left(\frac{4 \pi^2}{G (m+m)} \right ) (R+R)^3 = \left(\frac{16 \pi^2}{G m} \right ) R^3$$