What is the Rate of Change of Shadow Length with Distance from a Pole?

[physics604]

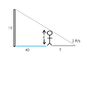
1. A street light is mounted at the top of a 15-ft-tall pole. A man 6 ft tall walks away from the pole with a speed of 5 fts along a straight path. How fast is the tip of his shadow moving when
he is 40 ft from the pole?

Homework Equations

$$x^2+y^2=z^2$$

The Attempt at a Solution

I've drawn a diagram so far (I've attached it to this thread), but I don't know where to start. Can someone give me a hint?

 

[Simon Bridge]

It would help to define some variables - let x=position of the man and y=position of the tip of his shadow.
So, off your diagram, s=y-x.

The question gives you dx/dt and asks you to find dy/dt.
If you can find a relationship between x and y, then you can find dy/dt in terms of dx/dt just by differentiating.
Hint: similar triangles.

 

[physics604]

Thanks! I got it!

$$25/3$$

 

[Simon Bridge]

Well done - don't forget your units.