What is the relationship between angle and static friction?

[Javad]

Homework Statement

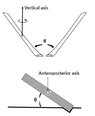
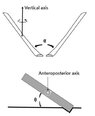
Two equal metal strips (each one 50cm) with different angles are pushed to slide on a straight surface by the equal forces F1 and F2 at t1, then we let them continue sliding. Object A slides with the velocity V’ and stops at t2 . Does the angle of ϴ have an effect on the velocity (V”) of object B? Which one would stop sooner (what is the relationship between traveling distance and forces)? Could we calculate the force along with object B? What is the difference between the friction forces? Is the equation ( F3 = F2 * Cosϴ ) correct?

Relevant Equations

F3 = F2 * Cosϴ

Fk = μk x N

 

[PeroK]

Can you post what you think of this problem?

 

[Javad]

Hi, I edited the question.

 

[Steve4Physics]

Hi @Javad. You need to tell use what you think the answers are. Or at least say what you have considered. Then you'll get feedback/guidance. See here: https://www.physicsforums.com/threads/homework-help-guidelines-for-students-and-helpers.686781/

Note:

1) The diagrams show forces marked $F_11$ and $F_12$ but it is unclear what these represent. Friction?

2) The purpose/meaning of F3 is unknown.

The meanings of any symbols you use should be clear.

Also, if this is a set problem, you should provide the original question, word-for-word. Sometimes posters misinterpret a question and only tell us their version. This can lead to chaos and confusion!

 

[Javad]

Hi, thank you, I edited the question.

Two equal metal strips (the same material, the same size and mass, mass for each one is 500 g, and size for each one is 50cm* 5cm) are pushed on a straight surface to reach the same velocity (V1 = 20m/s) at the same time (t1), then we let them freely continue sliding. Object A slides while the sliding direction is along the longitudinal centerline of the object, object B slides while there is an angle (ϴ = 45°) between the sliding direction and the longitudinal centerline of the object. Which object will stop sooner (which object will travel a shorter distance (d))?

d = vt + 1/2at²
d = 1/2 (v + v˳)t

 

[Steve4Physics]

Hi, thank you, I edited the question.

Two equal metal strips (the same material, the same size and mass, mass for each one is 500 g, and size for each one is 50cm* 5cm) are pushed on a straight surface to reach the same velocity (V1 = 20m/s) at the same time (t1), then we let them freely continue sliding. Object A slides while the sliding direction is along the longitudinal centerline of the object, object B slides while there is an angle (ϴ = 45°) between the sliding direction and the longitudinal centerline of the object. Which object will stop sooner (which object will travel a shorter distance (d))?

d = vt + 1/2at²
d = 1/2 (v + v˳)t

As already noted in Post #4, first you have to show that you have thought about the problem Any ideas?

Any particular issues that are stopping you from answering? You need to give us your own thoughts first, then we can try to help/guide.

 

[Javad]

Thank you for your patience, I suppose the traveling distance for object B would be shorter (means the object will stop sooner) because (after time t1) the forwarding force declines to zero faster in comparison with object A due to the angle ϴ , but I do not know the related equations. I want to learn how making angles on skis helps to reduce the velocity of a skier to stop.

 

[Steve4Physics]

Thank you for your patience, I suppose the traveling distance for object B would be shorter (means the object will stop sooner) because (after time t1) the forwarding force declines to zero faster in comparison with object A

What is producing this 'forwarding force'?
Suppose the surface were perfectly smootth, what would happen after t1?

 

[Javad]

We apply pushing force (F1 and F2) on the objects to reach the same velocity (V1), then they freely slide and finally stop. After t1 each object will lose the initial applied force, I suppose they will stop at two different locations because object B has angle ϴ and will travel a shorter distance.

 

[Steve4Physics]

I suppose they will stop at two different locations because object B has angle ϴ and will travel a shorter distance.

After t1, what force(s) act on each object?

 

[Javad]

There is no more extra force applying on the objects, they slide forward only by the initial force applied before t1 to reach the velocity (V1). But of course the friction force and air drag (please ignore the air drag) would work on both, however two objects are the same material on the same surface with the same coefficient of friction.

 

[Steve4Physics]

however two objects are the same material on the same surface with the same coefficient of friction.

Yes!
Q1. Does the magnitude of the friction force depend on angle θ?
Q2. Does the direction of the friction force depend on angle θ?
Q3. Apart from the force of friction, is any other force slowing the objects down?
If you can answer Q1-Q3, you're nearly there!

Here in the UK it's my bedtime! If I miss your next post, maybe someone else will come in. Otherwise any further replies from me will have to wait a few hours.

 

[Javad]

Yes!
Q1. Does the magnitude of the friction force depend on angle θ?
Q2. Does the direction of the friction force depend on angle θ?
Q3. Apart from the force of friction, is any other force slowing the objects down?
If you can answer Q1-Q3, you're nearly there!

Here in the UK it's my bedtime! If I miss your next post, maybe someone else will come in. Otherwise any further replies from me will have to wait a few hours.

Thank you for your time. Actually, I do not know the answers for all three questions, however as I know angle ϴ has no effect on the coefficient of friction, also we can ignore the question3. I think the correct answer should be in the concept of force vectors, like this equation Fᵪ=F.cosθ , while the moving direction is not at the same direction of force, more details are on this page (https://byjus.com/rajasthan-board/rbse-solutions-class-10-science-chapter-11/ ).

 

[Steve4Physics]

This is a ‘trick’ question designed to test your basic understanding.

Note that F1 and F2 have no effect after time t1. These forces have been removed so their components are irrelevant while the objects slow down.

Have another go….

Q1. Does the magnitude of the frictional force depend on angle θ?
Take a guess then click on the fuzzy text to reveal answer

No, The frictional force depends only on the coefficient of (kinetic) friction and on the normal reaction. The normal reaction equals each object’s weight in this problem. Therefore the magnitudes of the frictional forces are exactly the same for both objects.

Q2. Does the direction of the frictional force depend on angle θ?
Take a guess then click on the fuzzy text to reveal answer

No. The direction of the frictional force is opposite to the direction of motion. Since both objects move left, the frictional force on each object acts to the right.

Q3. Apart from the force of friction, is any other force slowing the objects down?
Take a guess then click on the fuzzy text to reveal answer

No, The frictional force is the only force slowing each object. Note: without the frictional force, each object would continue to move left with the same speed forever.

So you should now know that:
- the force making each object slow down is exactly the same for each object;
- the force making each object slow down does not depend on θ;
- you should also know each object decelerates according to F=ma where 'F' is the frictional force.

So what can you conclude about how far the two objects travel?

 

[Javad]

Thank you for the questions,

So we can calculate traveling distance by knowing the deceleration, and we can conclude the traveling distances for both objects are equal.

Based on this conclusion, why a skier makes skis like a pizza slice during the stop phase (attached images). I am not sure but it might the skis lose velocity based on the equation Fᵪ=F.cosθ . I appreciate hearing your idea.

 

[Steve4Physics]

Based on this conclusion, why a skier makes skis like a pizza slice during the stop phase (attached images). I am not sure but it might the skis lose velocity based on the equation Fᵪ=F.cosθ . I appreciate hearing your idea.

When changing the angle of the skis, skiers also make the leading edge of each ski 'dig' into the snow. This displaces snow, dissipating energy in the process. They have increased the coefficient of kinetic friction compared to a ski pointing forwards.

This is different to the problem you posted because (presumably) the surface in your problem is rigid (unlike snow).

(Also, when you write 'Fᵪ=F.cosθ', it is not clear what the force 'F' is. It can't be F1 or F2 because they have been 'switched off' after time t1. You need to understand the nature of each force acting to handle these sorts of problems.)

 

[Javad]

When changing the angle of the skis, skiers also make the leading edge of each ski 'dig' into the snow. This displaces snow, dissipating energy in the process. They have increased the coefficient of kinetic friction compared to a ski pointing forwards.

This is different to the problem you posted because (presumably) the surface in your problem is rigid (unlike snow).

(Also, when you write 'Fᵪ=F.cosθ', it is not clear what the force 'F' is. It can't be F1 or F2 because they have been 'switched off' after time t1. You need to understand the nature of each force acting to handle these sorts of problems.)

Ok, it makes sense, right now it is late time in San Diego, some hours later I will read all notes again and if I found a confusing thing I will back here for asking, thanks.

 

[jbriggs444]

They have increased the coefficient of kinetic friction compared to a ski pointing forwards.

I am not comfortable with this characterization.

Rather this suggests that the interaction of skis with snow is not properly described using the notion of a "coefficient of kinetic friction". There is no such coefficient. The relationship is not linear and does not depend on a single variable.

Technically, this is true of all friction. None of it is precisely described using a coefficient of friction. Much of it is approximated well in that manner.

 

[Steve4Physics]

I am not comfortable with this characterization.

Rather this suggests that the interaction of skis with snow is not properly described using the notion of a "coefficient of kinetic friction". There is no such coefficient. The relationship is not linear and does not depend on a single variable.

Technically, this is true of all friction. None of it is precisely described using a coefficient of friction. Much of it is approximated well in that manner.

I agree. Braking with skis on snow isn't simple 'sliding'; a simple coefficient of friction isn't applicable [edit - even as an empirical approximation].

I actually thought about this when writing the post. Initially I used 'effective coefficient’ (which isn’t too good) and then dropped ‘effective’ (even worse!) for brevity/simplicity.

The intention was to keep the explanation at (what I judged to be) the level the OP could fully understand.

 

[Javad]

When changing the angle of the skis, skiers also make the leading edge of each ski 'dig' into the snow. This displaces snow, dissipating energy in the process. They have increased the coefficient of kinetic friction compared to a ski pointing forwards.

This is different to the problem you posted because (presumably) the surface in your problem is rigid (unlike snow).

(Also, when you write 'Fᵪ=F.cosθ', it is not clear what the force 'F' is. It can't be F1 or F2 because they have been 'switched off' after time t1. You need to understand the nature of each force acting to handle these sorts of problems.)

Thank you for your time, I did not get the answer “does the angle ϴ have an effect on reduction the traveling distance of object B?”. I avoid interfering with the discussion about skiing. I posted one more thread for my problem, just by chance to hear more ideas.

https://www.physicsforums.com/threa...d-friction-force-on-a-sliding-object.1012020/

 

[Javad]

I am not comfortable with this characterization.

Rather this suggests that the interaction of skis with snow is not properly described using the notion of a "coefficient of kinetic friction". There is no such coefficient. The relationship is not linear and does not depend on a single variable.

Technically, this is true of all friction. None of it is precisely described using a coefficient of friction. Much of it is approximated well in that manner.

Thank you, could you please let me know an online reference to show the interaction of skis with snow at snowplouge position (forces acting on skis).

 

[jbriggs444]

Thank you, could you please let me know an online reference to show the interaction of skis with snow at snowplouge position (forces acting on skis).

You understand that essentially the whole point of skis is that they slide lengthwise easily while holding a line cross-wise? Same for ice skates and roller skates.

 

[Steve4Physics]

Thank you for your time, I did not get the answer “does the angle ϴ have an effect on reduction the traveling distance of object B?”. I avoid interfering with the discussion about skiing. I posted one more thread for my problem, just by chance to hear more ideas.

https://www.physicsforums.com/threa...d-friction-force-on-a-sliding-object.1012020/

The frictional force on each object is what causes it to slow down. So understanding the frictional force is the key to answering the question.

The frictional force on each object is F=μₖmg. Note that F does not depend on θ.
The acceleration of each object is a = F/m = μₖmg/m = μₖg.
In this question, since initial velocity is to the left, friction and acceleration act to the right.

This acceleration does not depend on θ so the objects have identical accelerations (or decelerations if you want to use that term). That means they stop in the same time and (their centres) move the same distance.

But note: the above describes the 'ideal' (introductory-level physics) way to consider the problem. It is a reasonable approximation to the 'real world' behaviour. But in the 'real world' the angle might have an effect. But the effect of different angles would be practically impossible to calculate; if you really needed to know the effect of angle, you would have to measure it experimentally.

 

[Javad]

The frictional force on each object is what causes it to slow down. So understanding the frictional force is the key to answering the question.

The frictional force on each object is F=μₖmg. Note that F does not depend on θ.
The acceleration of each object is a = F/m = μₖmg/m = μₖg.
In this question, since initial velocity is to the left, friction and acceleration act to the right.

This acceleration does not depend on θ so the objects have identical accelerations (or decelerations if you want to use that term). That means they stop in the same time and (their centres) move the same distance.

But note: the above describes the 'ideal' (introductory-level physics) way to consider the problem. It is a reasonable approximation to the 'real world' behaviour. But in the 'real world' the angle might have an effect. But the effect of different angles would be practically impossible to calculate; if you really needed to know the effect of angle, you would have to measure it experimentally.

sure, I will do this experiment some days later to see the effect of angle, thanks.

 

[Steve4Physics]

sure, I will do this experiment some days later to see the effect of angle, thanks.

An experiment with static friction would be easy to perform.

Get an adjustable inclined plane, e.g. a wooden plank with one end that can be raised/lowered and with the other end on the ground.

Place a ruler, aligned downhill, on the plane and adjust the plane’s angle (α to horizontal) until the ruler just starts to slide downhill. Note the value of α. For information, μₛ=tan(α).

Repeat with the same plane and ruler but with the ruler at different orientations (θ) with respect to the downhill direction.

(Good practice dictates that several repeat measurements should be done for each value of θ.)

Within the limits of experimental error, does changing θ change α?

It’s not the same as checking kinetic friction, but it would give an initial insight with little effort.