What is the relationship between voltage and flux in Faraday's Law?

[alan123hk]

A former colleague asked me a simple question about Faraday's law. As shown below, the configuration is just a circular conductor and a changing B field, and then tried to measure the voltage across the diameter. But I am not sure what the answer is?

Any help would be greatly appreciated.

 

[jtbell]

I am not sure what the answer is?

Nevertheless, what are your thoughts, uncertainties, etc., about it? Then people here can address them directly, and try to clear up any errors in your thinking, instead of simply giving you the answer (which is frowned upon here).

 

[hutchphd]

You nowhere say exactly how the B field is changing in time (uniformly?).
When you have a changing field like this it is no longer a "circuits' problem and you need to consider the fields explicitly. The reading on the voltmeter will depend upon the exact path of the wires, not just their topology. Are you assuming perfect symmetry? So make an analysis.
This is of course Walter Lewin's famous headscratcher.

 

[alan123hk]

Nevertheless, what are your thoughts, uncertainties, etc., about it? Then people here can address them directly, and try to clear up any errors in your thinking, instead of simply giving you the answer (which is frowned upon here).

Thanks for your reply.

My idea is that from the front view, there are two loops connected to the voltmeter, the EMF induced on the right side seems to be +0.5V, and the EMF induced on the left side seems to be -0.5V. There seems to be a contradiction, maybe there is no contradiction at all. I think it is possible to add two values. So the answer should be that the maximum chance is 0V.

Is my inference correct?

 

[alan123hk]

You nowhere say exactly how the B field is changing in time (uniformly?).
When you have a changing field like this it is no longer a "circuits' problem and you need to consider the fields explicitly. The reading on the voltmeter will depend upon the exact path of the wires, not just their topology. Are you assuming perfect symmetry? So make an analysis.
This is of course Walter Lewin's famous headscratcher.

You make a lot of sense. Let's assume that the B field changes linearly with time, so the induced E field is a constant value. The path of the voltmeter connection is shown in the diagram, which is vertically to the plane of the circular conductor and located behind it. In this way relative to the plane of two parallel connecting lines of the voltmeter, the left and right are completely symmetrical. Therefore, the connection line of the voltmeter should be perpendicular to the induced electric field, which means that no EMF will be generated on them.

In addition, of course the resistivity of each point of the circular conductor is also the same, and the internal resistance of the voltmeter is infinite, etc.

Please let me know any hints about the answer, thanks.

 

[vanhees71]

Of course it depends on the geometry of the wires connected to the volt meter. You don't have a voltage here but an EMF, because the electric field is not conservative since $\vec{\nabla} \times \vec{E}=-\partial_t \vec{B} \neq 0$. The volt meter in fact measures a (usually very small) current going through it. So you measure the EMF as calculated along the wires connecting the volt meter.

 

[hutchphd]

So the easy way for me to consider the problem is to realize (as @vanhees71 points out ) that the voltmeter in fact measures the current through it. Current is absolutely conserved and the net current through the meter in the symmetric case is the sum of two equal and opposite currents if one looks at the two smaller loops. So zero is the reading. Any asymmetry will likely produce a nonzero reading, but it will not properly be called a "Voltage" in the usual Kirchhof sense.

 

[alan123hk]

Of course it depends on the geometry of the wires connected to the volt meter. You don't have a voltage here but an EMF, because the electric field is not conservative since ∇→×E→=−∂tB→≠0. The volt meter in fact measures a (usually very small) current going through it. So you measure the EMF as calculated along the wires connecting the volt meter

I totally agree with your explanation, your explanation is very accurate and helpful.

So the easy way for me to consider the problem is to realize (as @vanhees71 points out ) that the voltmeter in fact measures the current through it. Current is absolutely conserved and the net current through the meter in the symmetric case is the sum of two equal and opposite currents if one looks at the two smaller loops. So zero is the reading. Any asymmetry will likely produce a nonzero reading, but it will not properly be called a "Voltage" in the usual Kirchhof sense.

Your explanation is very logical and reasonable. I think you may not intend to explain some details for the time being, but your explanation has no flaws anyway.

 

[Delta2]

So the easy way for me to consider the problem is to realize (as @vanhees71 points out ) that the voltmeter in fact measures the current through it. Current is absolutely conserved and the net current through the meter in the symmetric case is the sum of two equal and opposite currents if one looks at the two smaller loops. So zero is the reading. Any asymmetry will likely produce a nonzero reading, but it will not properly be called a "Voltage" in the usual Kirchhof sense.

I, on the other hand, believe that even in the case of asymmetry (that is even if we put the voltmeter leads anywhere along the circumference of the conductor) we will have again a zero reading, because there is no charge separation happening along the circumference of the conductor. A voltmeter measures indeed a current according to my opinion too, but this current must be a result of a scalar potential which is result of charge separation.

 

[hutchphd]

But the definition of a scalar potential assumes $\nabla \times \vec E =0$ so I don't know what scalar potential you mean. The internal workings of the Voltmeter in fact work by comparing magnetic force of an unknown current to a that of a spring

 

[vanhees71]

http://www.physics.princeton.edu/~mcdonald/examples/lewin.pdf

 

[alan123hk]

I personally tried to think more deeply about this problem, and believe that now I have found a very simple way to describe and predict the behavior of such circuits

I, on the other hand, believe that even in the case of asymmetry (that is even if we put the voltmeter leads anywhere along the circumference of the conductor) we will have again a zero reading, because there is no charge separation happening along the circumference of the conductor. A voltmeter measures indeed a current according to my opinion too, but this current must be a result of a scalar potential which is result of charge separation.

I think you made the very crucial point, that is, in fact, there is no charge separation happening along the circumference of the conductor, so from the perspective of the external circuit, there is no potential difference along the circumference of the circular conductor. This means that as long as the connecting wire of the voltmeter does not picked up the induced electric field generated by the changing magnetic field, regardless of the position of the connecting wire, the voltage measured by the voltmeter is still zero.

 

[hutchphd]

I would like to comment but I have no idea what you are saying:

This means that as long as the connecting wire of the voltmeter does not picked up the induced electric field generated by the changing magnetic field, regardless of the position of the connecting wire,

The Princeton citation from @vanhees71 is above is pretty comprehensive. Have at it.

 

[Delta2]

Well the paper states that
"The fact that the two meters give different readings when a = c and b = d (in sec. 2.1) indicates that the meter readings are not simply proportional to the electric scalar potential V at those points, as would be the case for a DC circuit"
I might be wrong in what i said in post #9 afterall.

 

[Delta2]

However the experiment setup is a bit different from what is discussed here so i am not completely sure.

 

[alan123hk]

I would like to comment but I have no idea what you are saying:

Sorry, my expression may not be clear enough, or I did not express my thoughts correctly.

Referring to the example I put forward on #1, the induced electric field generated by the changing B field will not only be concentrated on the circular conductor, but will also extend to all surrounding spaces, including the two connecting wires of the voltmeter.

What I mean is that since the circular conductor does not exert a potential difference on the two connecting wires, as long as the force of the induced electric field (generated by the changing B) acting on the charges on the two connecting wires does not generate a voltage across the voltmeter, the measured voltage on the voltmeter must be zero.

 

[Charles Link]

See https://www.physicsforums.com/threa...asure-a-voltage-across-inductor.880100/page-3 post 52 This is one of Professor Walter Lewin's videos.

 

[alan123hk]

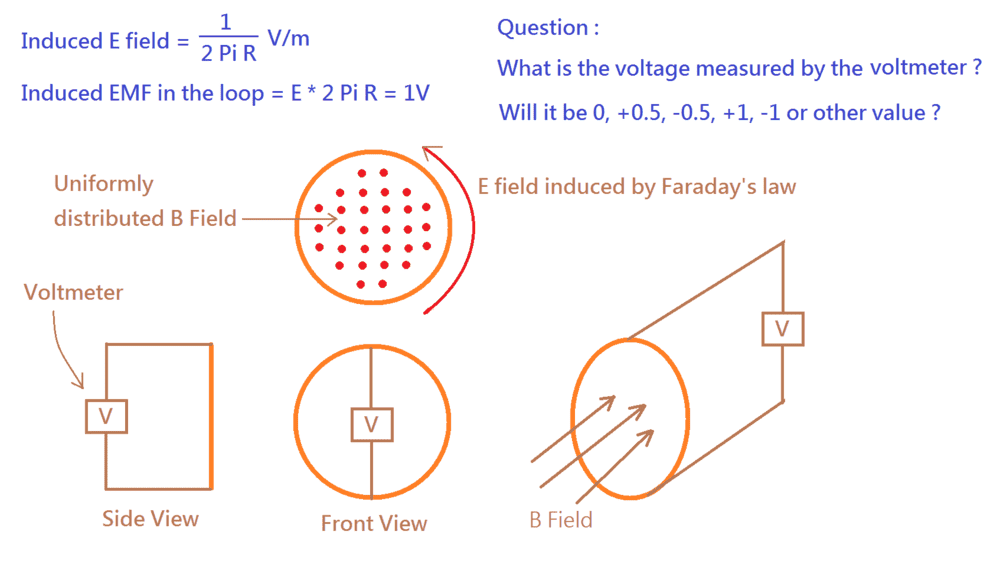
After rethinking this issue, I think that there is no paradox.

We should not treat a and b are exactly same, even if there is no voltage drop due to Ohm's law, there does exist an induced electric field between them, so they are indeed two different points.

As long as we define the Electromotive force (EMF) and PD (potential difference) as follows,

Electromotive force, $~EMF_{ab} =−\int_a^b E \cdot dl$
Potential difference, $~PD_{ab} = \int_a^b E \cdot dl$

and put the EMF (created by the induced electric field) into the equations, the correct calculation result can be obtained.

For example, we can easily prove that if the resistance of each point of the circular conductor is the same, there is indeed no potential difference along the circumference of the conductor.

Total length $~ L=\sum L_i$
Total EMF $~ \mathcal E=\sum \mathcal E_i=\sum C_1L_i$
Total Resistance $~R= \sum R_i= \sum C_2L_i$

where $~C_1$ and $C_2 ~$ are constants

For any arc length $~ L_i ~$ on the circumference, the actual potential difference should be : -

$$ \mathcal E_i - \frac {\sum \mathcal E_i} {\sum R_i} R_i$$
$$ C_1 Li - \frac {\sum C_1L_i} { \sum C_2L_i } ~ C_2L_i ~~ = ~ C_1 Li - \frac {C_1} { C_2 } ~ C_2L_i =~0 $$

 

[vanhees71]

Well the paper states that
"The fact that the two meters give different readings when a = c and b = d (in sec. 2.1) indicates that the meter readings are not simply proportional to the electric scalar potential V at those points, as would be the case for a DC circuit"
I might be wrong in what i said in post #9 afterall.

Sigh, well, I forgot that this imprecision is in this text. Please bear in mind that there is NO POTENTIAL in this case, because (in SI units)
$$\vec{\nabla} \times \vec{E}=-\partial_t \vec{B} \neq 0$$
and that's the reason why the meters in Lewin's example show different readings. What the (idealized) volt meter measures is the EMF (NOT VOLTAGE!) along the wires. Note that it's a CLOSED line integral:
$$\mathcal{E}=\int_{\text{wires}} \mathrm{d} \vec{r} \cdot \vec{E}=-\dot{\Phi}_{\vec{B}},$$
where $\Phi_{\vec{B}}$ is the magnetic flux through an arbitrary surface with the wires making its boundary (assuming that the wires are at rest).

 

[Delta2]

@vanhees71 the scalar potential is defined even in the case of $\nabla\times\vec{E}\neq\vec{0}$, simply by the solution to the wave equation (in the lorentz gauge)$$\nabla^2 V-\frac{1}{c^2}\frac{\partial^2 V}{\partial t^2}=-\frac{\rho}{\epsilon_0}$$ but of course as you notice the voltmeter doesn't measure that (it usually does but not in this weird setup).

 

[hutchphd]

What the (idealized) volt meter measures is the EMF (NOT VOLTAGE!) along the wires. Note that it's a CLOSED line integral:

I believe that part of the confusion in the OP is from the geometry of the Voltmeter as the nexus of two such closed curves of wire. For me it is easier to understand the measurement result as the sum of two opposite induced currents (but I have never been on really friendly terms with the EMF).

 

[vanhees71]

@vanhees71 the scalar potential is defined even in the case of $\nabla\times\vec{E}\neq\vec{0}$, simply by the solution to the wave equation (in the lorentz gauge)$$\nabla^2 V-\frac{1}{c^2}\frac{\partial^2 V}{\partial t^2}=-\frac{\rho}{\epsilon_0}$$ but of course as you notice the voltmeter doesn't measure that (it usually does but not in this weird setup).

That's of course true. I misunderstood the statement to mean a static potential such that $\vec{E}=-\vec{\nabla} V$, which is of course wrong in the general case. Here the relations of the em. field to the potentials is (in SI units)
$$\vec{E}=-\vec{\nabla} V-\partial_t \vec{A}, \quad \vec{B}=\vec{\nabla} \times \vec{A}.$$
In the Lorenz gauge
$$\Box V=\frac{1}{\epsilon_0} \rho, \quad \Box \vec{A}=\mu_0 \vec{j},$$
where the d'Alembert operator is defined as
$$\Box=\frac{1}{c^2} \partial_t^2 -\Delta.$$

 

[Charles Link]

The voltmeter is perhaps best modeled as a large resistor, with the voltage reading given by the product of the current and the voltage, as the resistance approaches infinity. The solution is to write out the loop equations, how Professor Lewin does, making sure to include any EMF from the changing magnetic flux, if it occurs inside the loop.
The location of the resistor of the voltmeter, along with the connecting leads, will affect what the voltmeter reads, rather than being able to assign a reading by just considering the two points in the circuit where the leads are attached.

 

[alan123hk]

I would like to express my views on the issue of non-conservative electric fields and potential differences.

Although the induced electric field is non-conservative, but for the fixed path and direction in the electric field, such as R1 and R2 shown in the figure below, there can indeed be a potential difference, because their voltage will respectively vary with their resistance, and they consume energy. But, of course, the placement and direction of the two voltmeters and their leads may affect the measured value.

Consider again the transformer shown in the figure, the secondary output voltage is also produced by the non-conservative electric field induced by changing magnetic field, therefore, its corresponding line integral of the electric field should only be along the path of the secondary coiled wire. If the line integral follows other paths, of course there may be different results.

In addition, We can see that the placement and direction of the secondary external output circuit loop has no (or extremely little) impact on the output voltage. The reason is obvious, because for the same magnetic flux , it only has one turn, but the number of turns inside the transformer is usually much larger than one turn.

 

[Charles Link]

For an inductor or transformer coil, there are a couple of ways to look at it. The method that I prefer is to observe that the electric field in the conductor must be nearly zero, so there must necessarily be a conservative field $E_s$ (electrostatic) in the coil that is equal and opposite the $E_{induced}$. The $E_{induced}$ is zero outside the component, but we can write $\oint E_s \cdot ds=0$ over a complete loop, so that if outside the inductor there is just a resistor, the voltage drop across the resistor must be equal to $\int E_{induced} \cdot ds$.
It perhaps is left to the reader to decide how they like to treat EMF's, e.g. $\mathcal{E}=-L di/dt$. The $E_{induced}$ behaves very differently from $E_s$ in that it is non-conservative. One method is to simply say the sum of the EMF's in a circuit loop is equal to the sum of the voltage drops. Alternatively one can write $\oint E_s \cdot ds=0$, and compute the $E_s$ in the inductor as just mentioned.

 

[hutchphd]

Thank you for sharing. If it gives you any solace, according to Prof Lewin's discussion of his experiences, there are MIT professors who are also similarly confused. The physics has been explained. A potential difference between points cannot depend upon the path.

 

[Delta2]

E hehe its good to know that not only us, the common mortals, but also professors at big universities get confused by this...

 

[alan123hk]

I want to further describe the secondary output of the transformer I mentioned.

Electromotive force = The line integral of the electric field along the coil including the final loop of the load.

Total resistance =coil resistance + load resistance

Current = Electromotive force divided by total resistance

When the coil resistance is much less than the load resistance, because the voltage drop of the coil resistance is very small, the output is almost equal to the EMF. In this situation we may say that the output is only EMF, although from the point of view of load resistance, there is still a voltage drop across it.

On the other hand, when the coil resistance is much larger than the load resistance, the output becomes almost equal to zero. In this case, we have to admit that the coil EMF driven by the non-conservative electric field is subtracted by the voltage drop caused by its own resistance and therefore the final output voltage becomes almost zero.

Therefore, my own conclusion is that although this may seem confusing, it may simply be because everyone in different situations may have different perspectives and priorities when dealing with the same issue.

Difference Between Electromotive Force & Potential Difference : -
https://circuitglobe.com/difference-between-electromotive-force-and-potential-difference.html

 

[hutchphd]

Their is a certain schadenfreude inherent but it also slightly disconcerting. This is a fundamental albeit subtle mistake for EE professors to screw up. I cannot find the source where Lewin discusses this but I remember it distinctly and will post it if I do.

...Its in his lecture see below in post #36

 

[Charles Link]

See https://www.physicsforums.com/threads/magnetic-flux-is-the-same-if-we-apply-the-biot-savart.927681/
for a very detailed discussion on transformers and other related topics. It's a rather lengthy thread, but you might find it a good source for some of the basic concepts as well as some of the finer details.