What Is the Torque Required by a Servo Motor?

[_Bd_]

Hi, I am working on a project that needs some rotation around a central axis. I was looking over at some Servos but I don't know how to calculate the torque required by the servo.

I was thinking of doing a simple free body diagram, but as I was drawing it I realized the forces are on the Z axis (assuming an X-Y plane), and therefore do not create a moment around the center axis of the servo, only moments I can think of are parallel to the shaft of the servo.

Heres a very crude image of what I'm trying to do.

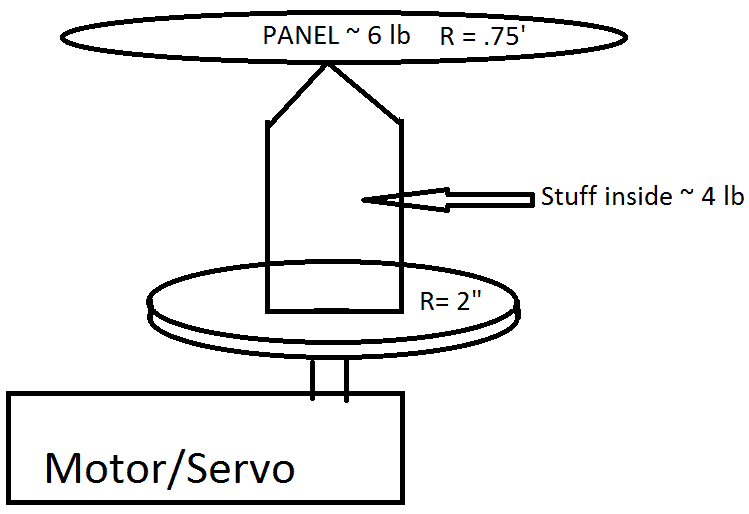
as mentioned, I tried to do a FBD but I couldn't really figure anything out of it. I am thinking it has to do only with the weight applied over the shaft and therefore it doesn't matter how close/far its from the central axis? just the amount pressing would generate more friction or something along those lines, but I'm kind of confused about this.I was thinking of using only T=Ia, (I for disk = 1/2 mr^2) and using m = m_disk + m_beam + m_bigdisk

but still, I don't knwo what alpha is (angular acceleration), I mean, I could probably use any servo's listed Torque and just get alpha from there, but that would be making the assumption that any servo, regardless of its torque output would be able to rotate that? (the idea doesn't make sense)

- Thank you for your help.

 

[Simon Bridge]

I don't knwo what alpha is (angular acceleration), I mean, I could probably use any servo's listed Torque and just get alpha from there, but that would be making the assumption that any servo, regardless of its torque output would be able to rotate that? (the idea doesn't make sense)

No - that makes perfect sense for your assumptions.

You are implicitly assuming that all the rotating components are perfectly balanced and that there is zero friction.
Under those conditions, absolutely any force or torque will produce some acceleration, however small.

You should measure the moment of inertia and the friction in your setup.
You can also expect your friction to increase change the speed of the rotations - ultimately getting higher so the device will reach a constant angular speed.

 

[_Bd_]

Thank you for the reply Simon,

Ok, so the moment of inertia would just be the sum of inertias of each component? (2 disks with I=1/2 mr^2) + (beam with I=1/12 mr^2) ? and I assume use the parallel axis theorem to move all inertias down to the bottom disk? (+1/2 md^2)and what would I do with those?, should I just plug those into the formula T= Ia ? (and plug in a desired alpha?).

What about if its not perfectly balanced, I mean this is going to be assembled by me, so even though I'll try to center it as much as possible, let's assume its not perfectly balanced, but close to, I know that would make the rotation not perfect around an axis, it would have certain pitch to the rotation, but will it drastically affect the torque required?

It doesn't matter if its not perfectly balanced as long as its not like completely horrid

 

[Simon Bridge]

Thank you for the reply Simon,

Ok, so the moment of inertia would just be the sum of inertias of each component? (2 disks with I=1/2 mr^2) + (beam with I=1/12 mr^2) ? and I assume use the parallel axis theorem to move all inertias down to the bottom disk? (+1/2 md^2)

... per your diagram, what is the axis of rotation? Do the disks not turn on the same axle through their centers?

and what would I do with those?, should I just plug those into the formula T= Ia ? (and plug in a desired alpha?).

Pretty much.

What about if its not perfectly balanced, I mean this is going to be assembled by me, so even though I'll try to center it as much as possible, let's assume its not perfectly balanced, but close to, I know that would make the rotation not perfect around an axis, it would have certain pitch to the rotation, but will it drastically affect the torque required?

It doesn't matter if its not perfectly balanced as long as its not like completely horrid

If it is not perfectly balanced you'll have a bit of a wobble - which will affect losses.
Losses in the system is why real life systems have a minimum torque to get them going and another minimum torque to keep moving.
If you have a lot of information you can model it - i.e. manufacturers should be able to tell you about the friction in their bearings. But, usually, this is something you measure on the finished product.

 

[_Bd_]

... per your diagram, what is the axis of rotation? Do the disks not turn on the same axle through their centers?

The axis of rotation is pretty much the center of the bottom disk (and its supposed to be aligned with the beam and the top disk).

Pretty much.

Ok, so then I'll start making specs on what alpha I want for this system.

Thank you again, you've been a lot of help

 

[Simon Bridge]

The axis of rotation is pretty much the center of the bottom disk (and its supposed to be aligned with the beam and the top disk).

Do you mean that the axis of rotation is through the center of all the disks, and perpendicular to the circular faces of the disks?

If so, then you don't need the parallel axis theorem.
All the rotation axes go through the centers of mass.

But if you mean that the axis of rotation goes through the bottom disk horizontally - then you will need the parallel axis theorem.

 

[_Bd_]

no no, axis of rotation goes normal (orthogonal) to the face of the disk, it is the shaft of the servo at the bottom that makes the whole thing rotate.

So just T=aI, where I is the sum of moments and a is the desired speed. . .hopefully this will get me going

 

[Simon Bridge]

That's correct - except a is the desired angular acceleration.