How to calculate required torque for a robot arm

[meakerb]

TL;DR Summary

I am trying to size the two motors needed for a robot arm I'm building. The pivot point for one motor is (through two pulleys) at the end of an arm driven by another motor.

I am trying to size the two motors needed for a robot arm I'm building.
The first motor, which I call the wrist motor, drives a pulley on a fixed axis that connects to a second pulley (of the same size) which is attached to a hand and load.

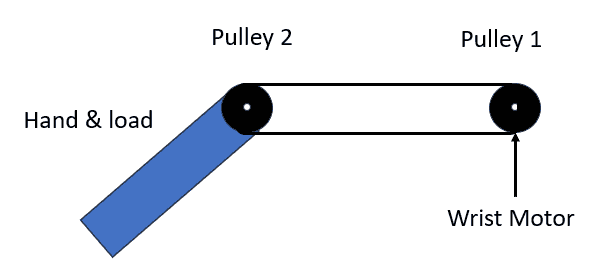
I can calculate the moment of inertia for the hand and load about the axis of the second pulley, and therefore calculate the required torque for the wrist motor.

However, the second motor, which I call the shoulder motor, also rotates on the same fixed axis as the wrist motor, but it rotates an arm that holds the second pulley.

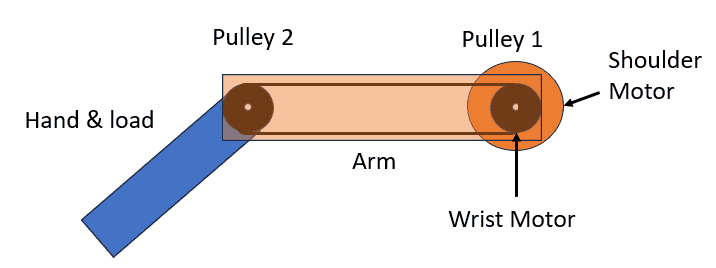
The first diagram, and my calculation for required torque for the wrist motor, assumed the shoulder motor was fixed (thereby fixing the axis of pulley 2). To calculate the required torque of the shoulder motor, do I assume that the wrist motor is fixed and use the parallel axis theroem for the moi of the hand & load, plus the moi of the arm? This doesn't seem right to me since, if the wrist motor is fixed, the gearing effect of the two pulleys will keep the hand & load at the same relative angle to the ground.

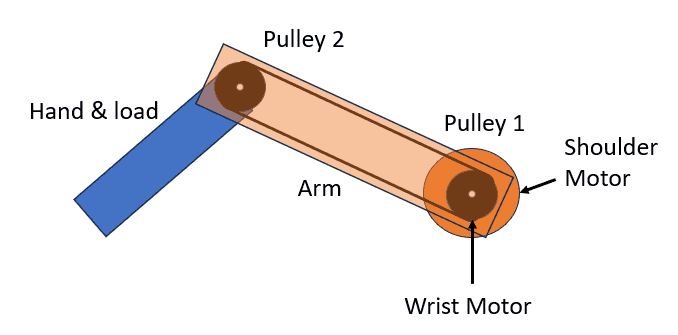
In reality, both motors will be moving at the same time. Any insight is greatly appreciated.

 

[erobz]

You have a motor bolted to a motor. If we imagine holding the shoulder motor still while rotating the wrist motor its clear that that any torque that is developed in the wrist motor, must be resisted by the shoulder motor. So...what happens when we start simultaneously rotating the shoulder motor. It seems clear to me that the shoulder motor (isolated from the system) has torque acting on it that depends on what the wrist motor is doing. How it all shakes out seems complicated at the moment.

I think we should start with a FBD of the blue arm at the end.

 

[jrmichler]

I am trying to size the two motors needed for a robot arm I'm building.

Any insight is greatly appreciated.

Since this is an engineering, as opposed to a physics problem, we need only find the worst case torque for each motor. That will be the case where:

The arm is horizontal
and
The hand is horizontal
and
The hand is holding the heaviest load with the center of gravity (CG) farthest out
and
The hand is accelerating clockwise at maximum $radians/sec^2$
and
The arm is accelerating clockwise at maximum $radians/sec^2$

There is more than one way to solve this. This is how I would attack the problem.

1) Given the maximum acceleration of the arm, calculate the vertical acceleration of the wrist joint in $inches/sec^2$
2) The torque at the wrist will be the value you calculated PLUS the vertical acceleration of the arm at the wrist times the distance to the hand/load CG times the mass of the hand/load. This is the required peak torque of the wrist motor.
3) Pretend that the wrist is locked in a straight line with the arm. Calculate the arm torque at maximum arm acceleration for that case. This calculation uses the total mass of the arm, hand, and load.
4) The peak torque requirement for the arm motor is the sum of the torques calculated in Steps 2 and 3.
5) The peak RPM of the arm motor is merely the maximum arm angular velocity.
6) The peak RPM of the wrist motor is calculated from the maximum hand angular velocity when the arm is moving at maximum angular velocity in the opposite direction.

This problem will benefit from careful step by step note taking. Diagrams are good.