What is the work energy theorem for a car at different distances?

[Llacrossedude]

1. Homework Statement
_>
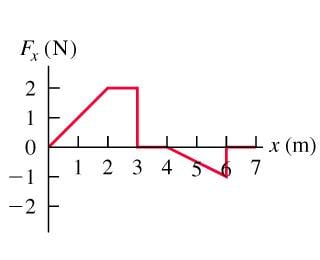
Suppose the 2.0kg model car is initially at rest at x=0 and F is the net force acting on it. Use the work energy theorem to find the speed of the car at (a) x=3.0m, (b) x=4.0m, and (c) x=7.0m.

2. Homework Equations

K_f-K_i
.5mv_f²-.5mv_i²
W=DeltaK
W=F*d

3. The Attempt at a Solution

3.0m
W=2N*3m=6J
W=.5(m)(v)²
v²=2W/m
v²=2(6J)/2.0kg
sqrt(6)=2.44m/s

4.0m
W=0N*4m=0J
W=.5(m)(v)²
v²=2W/m
v²=2(0J)/2.0kg
sqrt(0)=0m/s

7.0m
W=0N*4m=0J
W=.5(m)(v)²
v²=2W/m
v²=2(0J)/2.0kg
sqrt(0)=0m/s

Though it seems like the car slowing down there would still be work, so would the speed for both 4m and 7m both be 0m/s?

 

[madah12]

3.0m
W=2N*3m=6J
W=.5(m)(v)2
v2=2W/m
v2=2(6J)/2.0kg
sqrt(6)=2.44m/s
--------------------------
that is wrong because W is the area under the curve so for a constant force the height is the same so it is a rectangle with the area F*x
but here it is not a constant force you should take the area of a triangle till x =2 and from 2 to 3 a rectangle