What technique to integrate this function?

[member 428835]

Hi PF!

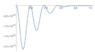
Attached are two plots of the same function, one uses a parameter $a=89.9$ and the other uses $a=89+9/10$. As you can see both functions are very different. Also, using NIntegrate over each gives two different outputs respectively, $-6.91846*10^{12},-6.91949*10^{19}$.

My question is, how do I know if either is right, and if so which one? I'm obviously leaning towards the non-floating point $a=89+9/10$ as the more correct, but how do I know this integral is even right at all?

Are there other numerical integration strategies I should look at besides NIntegrate?

 

[jedishrfu]

You could compare the two a values. While they may appear the same, they may instead be subtly different in the lowest bits.

Try a1 - a2 and see if it’s a zero or some small number. Base 10 numbers don’t always map to binary well.

 

[member 428835]

You could compare the two a values. While they may appear the same, they may instead be subtly different in the lowest bits.

Try a1 - a2 and see if it’s a zero or some small number. Base 10 numbers don’t always map to binary well.

Mathematica outputs 0. (the decimal after the zero indicates a float.) I tell Mathematica to output more digits and it does not output anything. There has to be some difference though, at least in how the function reads each.

 

[eys_physics]

Could you give the expressions for the functions which are compared or are they only known explicitly (e.g. a solution to an equation)?
Also, it seems like the functions have very large amplitudes. Perhaps, you should do some re-scaling. Otherwise, you might loose precision.
It looks like the amplitudes of the functions are very sensitive to the parameter $a$.

 

[member 428835]

Could you give the expressions for the functions which are compared or are they only known explicitly (e.g. a solution to an equation)?
Also, it seems like the functions have very large amplitudes. Perhaps, you should do some re-scaling. Otherwise, you might loose precision.
It looks like the amplitudes of the functions are very sensitive to the parameter $a$.

I could give the expressions but they're way too many terms to be meaningful. A bunch of sines and cosines. But there are s TON of them.
Yes, I agree that the functions are very sensitive to $a$.

 

[Dale]

With such a sensitive integrand and such large numbers it is unlikely that either integral is meaningful.

 

[member 428835]

With such a sensitive integrand and such large numbers it is unlikely that either integral is meaningful.

Is there a way to get a good feel for when an integral is not meaningful? See, the integral is a matrix component of an algebraic eigenvalue problem $K = \lambda M$, which for this case was the $1,1$ component of a $5\times 5$ matrix. It turns out it did not matter whether I used the float or exact number, because I received the same $\lambda$ for each case.

What's happening?

 

[Dale]

Plot lots of variations and see if the results make sense. If they do then it is probably meaningful.

 

[George Jones]

I tell Mathematica to output more digits and it does not output anything.

What does this mean? You made Mathematica do all floating point calculations with more (decimal) digits? You did not change the number of digits for calculations, but you displayed more output digits?

I am unfamiliar with Mathematica, but I have used Maple extensively. Maple has a control variable, Digits, that sets the number of digits used in floating point calculations. The default value of Digits is 10. I have found that setting Digits to 20 or 30 can wildly change the value of a sensitive sum in which terms have different signs.

 

[member 428835]

What does this mean? You made Mathematica do all floating point calculations with more (decimal) digits? You did not change the number of digits for calculations, but you displayed more output digits?

Yea, I displayed more digits for the 89+9/10 - 89.9, but did not send a command about the amount of digits to be used for floats.

I am unfamiliar with Mathematica, but I have used Maple extensively. Maple has a control variable, Digits, that sets the number of digits used in floating point calculations. The default value of Digits is 10. I have found that setting Digits to 20 or 30 can wildly change the value of a sensitive sum in which terms have different signs.

Does anyone know how to do this in Mathematica, and what the default is set to?

 

[eys_physics]

Yes, Mathematica has a parameter called WorkingPrecision, see https://reference.wolfram.com/language/ref/WorkingPrecision.html. One suggestion to joshmccraney could be to play a bit with that parameter.

 

[member 428835]

Yes, Mathematica has a parameter called WorkingPrecision, see https://reference.wolfram.com/language/ref/WorkingPrecision.html. One suggestion to joshmccraney could be to play a bit with that parameter.

Thanks. I'll look into that. Do you know if this is at all similar to setting accuracy goals for numerical integration, say MaxRecursion for example?

 

[George Jones]

Does anyone know how to do this in Mathematica, and what the default is set to?

After taking less than 5 seconds to try

mathematica calculations digits

in Google, I found

https://reference.wolfram.com/language/tutorial/NumericalPrecision.html