Mathematica Numerical vs. Monte-Carlo Simulations

[EngWiPy]

It's histogram(x). When I used with the data I have, I got the attached figure. Does that make sense?

 

[Dale]

It's histogram(x). When I used with the data I have, I got the attached figure. Does that make sense?

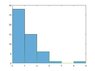
Yes, that seems right. Notice how it does not go out to infinity and how it is not strictly monotonically decreasing. The variations are small, but they will make a difference in achieving a given level of numerical precision.

 

[EngWiPy]

Yes, that seems right. Notice how it does not go out to infinity and how it is not strictly monotonically decreasing. The variations are small, but they will make a difference in achieving a given level of numerical precision.

Can I do anything about it? I'm writing a scientific journal, do you think such justification is acceptable for why there is a difference between the two curves?

 

[Dale]

Hmm, OK, if you are writing a scientific paper then you want to hold your work to a higher standard. Let's look at a couple more things.

First, instead of generating 1,000,000 numbers that are exponentially distributed and plotting the histogram of the distribution, let's investigate the sampling distribution. Instead of 1,000,000 numbers, generate 1,000 sets of 1,000 numbers each. For each set calculate the mean and the standard deviation (1,000 means and 1,000 standard deviations) and then plot the histograms of those. Let's see if there is any bias.

Second, see if you can easily get a qq plot in Matlab.

 

[EngWiPy]

In the first figure, I didn't generate $10^6$ samples. In the attached figure I did. Does this change anything before going to implement your suggestion?

 

[Dale]

In the first figure, I didn't generate $10^6$ samples. In the attached figure I did. Does this change anything before going to implement your suggestion?

No. It still shows the same key features, but it is smaller and harder to see. The range is not infinite and the curve is not smooth. This is to be expected in any random number generator, but it is a source of numerical error.

If we are lucky then the sampling distribution will show some small bias.

 

[EngWiPy]

OK, I did your suggestion, and got the attached figures for the mean and standard deviation. What can we infer from this?

 

[EngWiPy]

Also attached are the qq plot for the means and standard deviations calculated above

 

[Dale]

So it looks like the RNG is not too bad but the sampling distribution does show a bit heavier tails than normal and a bit of right skew.

Can you do a qq plot of the ySim against the exponential distribution instead of the normal distribution?

Also, what is the mean and standard deviation of the sampling distribution of the mean?

 

[EngWiPy]

So it looks like the RNG is not too bad but the sampling distribution does show a bit heavier tails than normal and a bit of right skew.

Q1: Can you do a qq plot of the ySim against the exponential distribution instead of the normal distribution?

Q2: Also, what is the mean and standard deviation of the sampling distribution of the mean?

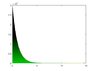
I didn't understand your questions. For Q1: What do you mean by qq plotting ySim against the exponential distribution? and how? I qq plot ySim alone and got the attached figure.

I also didn't understand Q2. Sorry, but can you elaborate, please.

 

[EngWiPy]

OK, for Q2: the mean and the standard deviation of the mean are 1.0001 and 0.0309, respectively.

 

[Dale]

OK, for Q2: the mean and the standard deviation of the mean are 1.0001 and 0.0309, respectively.

OK, that is essentially unbiased.

 

[EngWiPy]

So, what is the implication of this on my result?

 

[Dale]

I didn't understand your questions. For Q1: What do you mean by qq plotting ySim against the exponential distribution? and how? I qq plot ySim alone and got the attached figure

So the qq plots you have posted so far plot against the normal distribution. The ySim values are not normally distributed so the qq plot should be done against the exponential distribution.

 

[Dale]

It should be some sort of an option to plot against different distributions.

 

[EngWiPy]

Right. I did it, and got the attached figure.

 

[Dale]

Good. Do you see the deviations on the upper right and how there is some discrete steps where there are 4 points with the same vertical position? The errors from that are not well characterized. So I think you can justify not using the Monte Carlo.

It appears that there is not much, if any, bias in the sampling distribution, but the asymmetric numerical errors make those results suspicious.

 

[EngWiPy]

I need to use Monte Carlo simulations as an independent verification of my results. To the best of my knowledge in my field, unless there is some numerical approximation in the mathematical analysis, Monte Carlo simulations give accurate results. I'm not sure why it's not the case here. I'm concerned that my paper will be rejected because of this simulation only, as I think the mathematical analysis is correct. I forgot if we discussed this before, but is the Monte Carlo simulation procedure I described in the other thread (see post #5) correct?

 

[EngWiPy]

Any comment on this? Is it acceptable to say on a scientific article that the small discrepancy in results is due to some inaccuracy in the simulations?

 

[mfig]

Is it acceptable to say on a scientific article that the small discrepancy in results is due to some inaccuracy in the simulations?

What is the small discrepancy? 1 part in 1 million? 1 part in 1 billion? Is there some reason you are using an exponential distribution and not a uniform distribution for your sampling? If you post just the MC integration code, we might be able to see a problem with it.

 

[torquil]

Could it be due to an accumulation of rounding errors? This can happen when you try to add a lot of very small numbers to a large number. See the first two items in the list on page 2 in this PDF:

https://www.google.no/url?sa=t&rct=...0zK3Z2x4EE9nJ0DI8Y282w&bvm=bv.123664746,d.bGs

 

[EngWiPy]

What is the small discrepancy? 1 part in 1 million? 1 part in 1 billion? Is there some reason you are using an exponential distribution and not a uniform distribution for your sampling? If you post just the MC integration code, we might be able to see a problem with it.

See this thread for more details. The discrepancy is shown on the figure attached on post #41. Mathematica code can be found on post #35.

 

[mfig]

Mathematica code can be found on post #35.

Thanks, but I was asking about the Monte-Carlo code for the integration. If you post this code, someone might be able to see a shortcoming in the code, or explain the discrepancy.

 

[EngWiPy]

I explained the steps of Monte-Carlo simulations on post # 35 I believe. The rest are just semantics. Monte-Carlo is not for the integration by the way. But rather simulation of the same metric as the integration tries to evaluate. This is the idea behind it; to have two independent methods to evaluate the same quantity. I don't have the code at hand right now, but I will try to post it if necessary.

 

[mfig]

Monte-Carlo is not for the integration by the way.

I see. I was under the impression you were comparing the results of some numerical integration technique to a MC integration method. Now that I know there are other, unseen, codes involved somewhere along the way I see no way of relating the results of the numerical integration technique mentioned in the first post to the results of some other simulation involving a MC technique somehow. :(

Good luck!

 

[Dale]

Any comment on this? Is it acceptable to say on a scientific article that the small discrepancy in results is due to some inaccuracy in the simulations?

I wouldn't even report the Monte Carlo results. I don't trust them. There are too many unknowns and uncontrolled errors.

 

[EngWiPy]

I wouldn't even report the Monte Carlo results. I don't trust them. There are too many unknowns and uncontrolled errors.

But it's a good practice in my field to verify the numerical results. Most reviewers don't follow the mathematical derivations, and judge by the results and the general trend.

 

[Dale]

Isn't your whole concern that the Monte Carlo simulation does not verify your result?

In any case, the Monte Carlo is also a numerical result, so how can you use one numerical result to verify another. Since the two methods disagree then there are two possibilities, either you made a mistake in the code or numerical errors are causing the disagreement. If the disagreement is due to numerical errors then the problem is in the Monte Carlo since it does not control numerical errors.

 

[EngWiPy]

Isn't your whole concern that the Monte Carlo simulation does not verify your result?

In any case, the Monte Carlo is also a numerical result, so how can you use one numerical result to verify another. Since the two methods disagree then there are two possibilities, either you made a mistake in the code or numerical errors are causing the disagreement. If the disagreement is due to numerical errors then the problem is in the Monte Carlo since it does not control numerical errors.

If the discrepancy is huge or not constant, then yes, I would say there is something wrong definitely. But the discrepancy is very small and constant. By numerical I meant plotting a mathematical equation vs. averaging which is the case in Monte Carlo simulations. Both are two different and independent methods to evaluate the same results. Monte Carlo is a verification in this sense. You are right though, I might have made a mistake. In that case I haven't found it.