- #1
Karol
- 1,380
- 22
Homework Statement
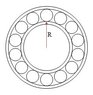
The outer ring is rotating, the inner is fixed. n is the number of balls of radius r and mass m. the outer shell has mass M. the bearing (the outer shell) rotates with angular velocity Ω. what's it's kinetic energy.
Homework Equations
Moment of inertia of a ball: ##I=\frac{2}{5}mr^2##
Moment of inertia of a thin ring: ##I=Mr^2##
Energy of a rigid body: ##E=\frac{1}{2}I\omega^2##
3. The Attempt at a Solution
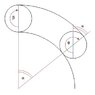
When a ball rotates an angle β and advances through angle α, it actually rotates ##\theta=\beta+\alpha##
Relation between α and β: ##s=\alpha R=\beta r\; \rightarrow\; \beta=\frac{R}{r}\alpha##
$$\dot \theta=\dot\alpha\left( 1+\frac{R}{r} \right)$$
I mark with ω the actual angular velocity of a ball and so:
$$\dot \theta=\omega,\; \dot\alpha=\Omega\; \rightarrow\; \omega=\Omega\left( 1+\frac{R}{r} \right)$$
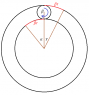
$$E=\frac{1}{2}I_{ball}\omega^2+\frac{1}{2}I_{ring}\Omega^2$$
$$E=\frac{1}{2}\left[\left(1+ \frac{2}{5} \right) nmr^2\left( 1+\frac{R}{r} \right)^2\Omega^2+M(R+2r)^2\Omega^2 \right]$$
$$E=\frac{\Omega^2}{2}\left[\left(1+ \frac{2}{5} \right)nm\left( 1+\frac{R}{r} \right)^2r^2+M(R+2r)^2 \right]$$
Attachments
Last edited: