SUMMARY
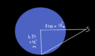
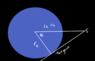
The discussion focuses on determining the geographic locations on Earth where a geostationary satellite, positioned at an altitude of 35,860 kilometers, is not visible. It is established that locations near the poles cannot see the satellite due to the curvature of the Earth, as observers would need to look through the planet. The correct mathematical relationship for visibility is defined as cos(angle of latitude or longitude) = Radius of Earth / (Height of satellite + Radius of Earth), which clarifies the conditions under which visibility is possible.
PREREQUISITES
- Understanding of geostationary satellites and their altitude (35,860 kilometers)
- Basic knowledge of Earth's radius (6,371 kilometers)
- Familiarity with trigonometric functions, specifically cosine
- Ability to interpret and create geometric diagrams
NEXT STEPS
- Research the mathematical principles behind satellite visibility and Earth curvature
- Explore the concept of geostationary orbit and its applications
- Learn about the impact of latitude on satellite visibility
- Investigate other types of satellite orbits and their visibility constraints
USEFUL FOR
Students studying astronomy, physics enthusiasts, and professionals in satellite communications who need to understand satellite visibility and geostationary orbit mechanics.