Where to Begin with Integrals to Integration by Parts

  • Context: High School 
  • Thread starter Thread starter russia123
  • Start date Start date
  • Tags Tags
    Integral
Click For Summary

Discussion Overview

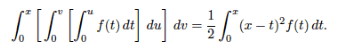
The discussion revolves around the topic of integrals, specifically focusing on techniques for solving them, including integration by parts. Participants express their struggles with the subject and explore various approaches to tackle a particular integral problem.

Discussion Character

  • Exploratory, Technical explanation, Homework-related

Main Points Raised

  • One participant expresses confusion about where to start with integrals, indicating a lack of confidence in the topic.
  • Another participant introduces the Cauchy formula for iterated integrals and suggests focusing on the right-hand side of an exam question, prompting a discussion on applicable techniques.
  • A participant proposes expanding the expression (x-t)^2 and separating the integrals based on addition as a potential method to solve the problem.
  • In response, another participant advises against expansion and hints at using a function g(t) to inspire further thought.
  • Finally, a participant recalls that integration by parts is a relevant technique, acknowledging a previous oversight.

Areas of Agreement / Disagreement

The discussion reflects a lack of consensus on the best approach to the integral problem, with some participants advocating for expansion while others suggest alternative methods like integration by parts.

Contextual Notes

Participants have not fully explored the implications of their proposed methods, and there are unresolved assumptions regarding the definitions and applications of the techniques discussed.

Who May Find This Useful

Individuals seeking to understand integral techniques, particularly those struggling with foundational concepts or preparing for exams in calculus.

russia123
Messages
5
Reaction score
0
I've looking at this and I'm dumbfound as to where to begin. Integrals have never been my strong suit.

iefdoh.jpg
 
Physics news on Phys.org
This is called the Cauchy formula for iterated integrals (don't mix it up with the Cauchy formula in complex analysis). Ignore the left hand side. Suppose you were asked to answer the right hand side in an exam. What techniques do you know which would help you?
 
What I had in mind is expanding the (x-t)^2, and then multiplying everything out, and then I would have 3 separate integrals due to being able to separate integrals based on addition.
 
No, don't expand. If I wrote (x-t)2 = g(t), would that give you ideas?
 
Ah, integration by parts is the first thing that comes to mind. Don't know how I missed that.
 

Similar threads

High School Integration by parts of inverse sine, a solved exercise, some doubts...
  • · Replies 4 ·
Replies
4
Views
3K
High School Straightforward integration…
  • · Replies 27 ·
Replies
27
Views
3K
Undergrad Integrating a product of exponential and trigonometric functions
  • · Replies 21 ·
Replies
21
Views
4K
High School Integration by Parts, an introduction I get confused with
  • · Replies 2 ·
Replies
2
Views
3K
High School Why is the definite integral of 1/x from -1 to 1 undefined?
  • · Replies 4 ·
Replies
4
Views
6K
Undergrad Ambiguity of the term "indefinite integral"
  • · Replies 11 ·
Replies
11
Views
2K
High School Question about the limits of integration in a change of variables
  • · Replies 2 ·
Replies
2
Views
3K
High School Why don't we account for the constant in integration by parts?
  • · Replies 16 ·
Replies
16
Views
4K
High School Does U-Substitution Function as the Inverse of the Chain Rule?
  • · Replies 10 ·
Replies
10
Views
3K
Undergrad Did Math DF's integral calculator make a glaring mistake?
  • · Replies 8 ·
Replies
8
Views
3K